Niels Bohr

In 1913 one of Rutherford's students, Niels Bohr, proposed a model for the hydrogen atom that was consistent with Rutherford's model and yet also explained the spectrum of the hydrogen atom. The Bohr model was based on the following assumptions.

1. The electron in a hydrogen atom travels around the nucleus in a circular orbit.

2. The energy of the electron in an orbit is proportional to its distance from the nucleus. The further the electron is from the nucleus, the more energy it has.

3. Only a limited number of orbits with certain energies are allowed. In other words, the orbits are quantized.

4. The only orbits that are allowed are those for which the angular momentum of the electron is an integral multiple of Planck's constant divided by 2.

5. Light is absorbed when an electron jumps to a higher energy orbit and emitted when an electron falls into a lower energy orbit.

6. The energy of the light emitted or absorbed is exactly equal to the difference between the energies of the orbits.

Some of the key elements of this hypothesis are illustrated in below. Three points deserve particular attention. First, Bohr recognized that his first assumption violates the principles of classical mechanics. But he knew that it was impossible to explain the spectrum of the hydrogen atom within the limits of classical physics. He was therefore willing to assume that one or more of the principles from classical physics might not be valid on the atomic scale.

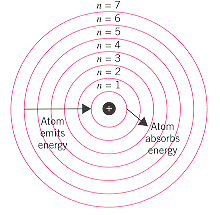
fig6_13.gif (8612 bytes)

According to the the Bohr model, hydrogen atoms absorb light when an electron is excited from a low-energy orbit (such as n = 1) into a highter energy orbit (n = 3). Atoms that have been excited by an electric discharge can give off light when an electron drops from a high-energy orbit (such as n = 6) into a lower energy orbit (such as n = 1). the energy of the photon absorbed or emitted when the electron moves from one orbit to another is equal to the difference between the energies of the orbits.

Second, he assumed there are only a limited number of orbits in which the electron can reside. He based this assumption on the fact that there are only a limited number of lines in the spectrum of the hydrogen atom and his belief that these lines were the result of light being emitted or absorbed as an electron moved from one orbit to another in the atom.

Finally, Bohr restricted the number of orbits on the hydrogen atom by limiting the allowed values of the angular momentum of the electron. Any object moving along a straight line has a momentum equal to the product of its mass (m) times the velocity (v) with which it moves. An object moving in a circular orbit has an angular momentum equal to its mass (m) times the velocity (v) times the radius of the orbit (r). Bohr assumed that the angular momentum of the electron can take on only certain values, equal to an integer times Planck's constant divided by 2.

Bohr then used classical physics to show that the energy of an electron in any one of these orbits is inversely proportional to the square of the integer n. The difference between the energies of any two orbits is therefore given by the following equation.

In this equation, n₁ and n₂ are both integers and R_H is the proportionality constant known as the Rydberg constant.

Planck's equation states that the energy of a photon is proportional to its frequency.

Substituting the relationship between the frequency, wavelength, and the speed of light into this equation suggests that the energy of a photon is inversely proportional to its wavelength. The inverse of the wavelength of electromagnetic radiation is therefore directly proportional to the energy of this radiation. By properly defining the units of the constant, R_H, Bohr was able to show that the wavelengths of the light given off or absorbed by a hydrogen atom should be given by the following equation.

Bohr was able to show that the wave-lengths in the UV spectrum of hydrogen discovered by Lyman correspond to transitions from one of the higher energy orbits into the n = 1 orbit. The wavelengths in the visible spectrum of hydrogen analyzed by Balmer are the result of transitions from one of the higher energy orbits into the n = 2 orbit. The Paschen, Brackett, and Pfund series of lines in the infrared spectrum of hydrogen result from electrons dropping into the n = 3, n = 4, and n = 5 orbits, respectively.

The Bohr model did an excellent job of explaining the spectrum of a hydrogen atom. By incorporating a Z² term into the equation, which adjusted for the increase in the attraction between an electron and the nucleus of the atom as the atomic number increased, it could even explain the spectra of ions that contain one electron, such as the He⁺, Li²⁺, and Be³⁺ ions. Nothing could be done, however, to make this model fit the spectra of atoms with more than one electron. The Bohr model left two important questions unanswered. Why are there only a limited number of orbits in which the electron can reside in a hydrogen atom? And, why can't this model be extended to many-electron atoms?