Jacques-Alexandre-CÚsar Charles
Charles' Law
(Jacques-Alexandre-CÚsar Charles)
On 5 June 1783, Joseph and tienne Montgolfier used a fire to inflate a spherical
balloon about 30 feet in diameter that traveled about a mile and one-half before it came
back to earth. News of this remarkable achievement spread throughout France, and
Jacques-Alexandre-CÚsar Charles immediately tried to duplicate this performance. As a
result of his work with balloons, Charles noticed that the volume of a gas is directly
proportional to its temperature.
V a T
This relationship between the temperature and volume of a gas, which became known as
Charles' law, provides an explanation of how hot-air balloons work. Ever since the third
century B.C., it has been known that an object floats when it weighs less than the fluid
it displaces. If a gas expands when heated, then a given weight of hot air occupies a
larger volume than the same weight of cold air. Hot air is therefore less dense than cold
air. Once the air in a balloon gets hot enough, the net weight of the balloon plus this
hot air is less than the weight of an equivalent volume of cold air, and the balloon
starts to rise. When the gas in the balloon is allowed to cool, the balloon returns to the
ground.
Charles' law can be demonstrated with the apparatus shown below. A 30-mL syringe and a
thermometer are inserted through a rubber stopper into a flask that has been cooled to
0║C. The ice bath is then removed and the flask is immersed in a warm-water bath. The gas
in the flask expands as it warms, slowly pushing the piston out of the syringe. The total
volume of the gas in the system is equal to the volume of the flask plus the volume of the
syringe. The table below contains typical data obtained with this apparatus.
 |
The Dependence of the Volume of
a Gas on its Temperature
| Temperature (║C) |
Volume (mL) |
| 0 |
107.9 |
| 5 |
109.7 |
| 10 |
111.7 |
| 15 |
113.6 |
| 20 |
115.5 |
| 25 |
117.5 |
| 30 |
119.4 |
| 35 |
121.3 |
| 40 |
123.2 |
|
| Charles' law can be demonstrated with the apparatus shown here. When
the flask is removed from the ice bath and placed in a warm-water bath, the gas in the
flask expands, slowly pushing up on hte piston of the syringe. |
The graph below shows a plot of the data above. This graph provides us with another way
of defining absolute zero on the temperature scale. Absolute zero is the temperature at
which the volume of a gas becomes zero when the a plot of the volume versus temperature
for a gas are extrapolated. As expected, the value of absolute zero obtained by
extrapolating the data in the table abobe is essentially the same as the value
obtained from the graph of pressure versus temperature in the preceding section. Absolute
zero can therefore be more accurately defined as the temperature at which the pressure and
the volume of a gas extrapolate to zero.
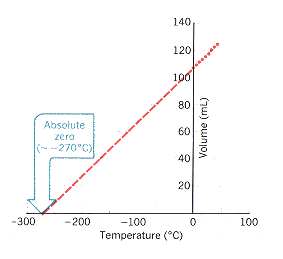 |
When data obtained with the Charles' law apparatus in Figure 4.9 are extrapolated, the
volume of the gas approaches zero when the temperature of the gas is approximately
-270║C. |
When the temperatures in the table above are converted from the Celsius to the Kelvin
scale, a plot of the volume versus the temperature of a gas becomes a straight line that
passes through the origin. Any two points along this line can therefore be used to
construct the following equation, which is known as Charles' law.
Before using this equation, it is important to remember that temperatures must be
converted from ║C to K.


