| The Activation Energy of Chemical Reactions | Catalysts and the Rates of Chemical Reactions | Determining the Activation Energy of a Reaction |
The Activation Energy of Chemical Reactions
Only a small fraction of the collisions between reactant molecules convert the reactants into the products of the reaction. This can be understood by turning, once again, to the reaction between ClNO2 and NO.
ClNO2(g) + NO(g) ![]() NO2(g)
+ ClNO(g)
NO2(g)
+ ClNO(g)
In the course of this reaction, a chlorine atom is transferred from one nitrogen atom to another. In order for the reaction to occur, the nitrogen atom in NO must collide with the chlorine atom in ClNO2.
Reaction won't occur if the oxygen end of the NO molecule collides with the chlorine atom on ClNO2.
Nor will it occur if one of the oxygen atoms on ClNO2 collides with the nitrogen atom on NO.
Another factor that influences whether reaction will occur is the energy the molecules carry when they collide. Not all of the molecules have the same kinetic energy, as shown in the figure below. This is important because the kinetic energy molecules carry when they collide is the principal source of the energy that must be invested in a reaction to get it started.

The overall standard free energy for the reaction between ClNO2 and NO is favorable.
| ClNO2(g) + NO(g) |
But, before the reactants can be converted into products, the free energy of the system must overcome the activation energy for the reaction, as shown in the figure below. The vertical axis in this diagram represents the free energy of a pair of molecules as a chlorine atom is transferred from one to the other. The horizontal axis represents the the sequence of infinitesimally small changes that must occur to convert the reactants into the products of this reaction.

To understand why reactions have an activation energy, consider what has to happen in order for ClNO2 to react with NO. First, and foremost, these two molecules have to collide, thereby organizing the system. Not only do they have to be brought together, they have to be held in exactly the right orientation relative to each other to ensure that reaction can occur. Both of these factors raise the free energy of the system by lowering the entropy. Some energy also must be invested to begin breaking the Cl-NO2 bond so that the Cl-NO bond can form.
NO and ClNO2 molecules that collide in the correct orientation, with enough kinetic energy to climb the activation energy barrier, can react to form NO2 and ClNO. As the temperature of the system increases, the number of molecules that carry enough energy to react when they collide also increases. The rate of reaction therefore increases with temperature. As a rule, the rate of a reaction doubles for every 10oC increase in the temperature of the system.
Purists might note that the symbol used to represent the difference
between the free energies of the products and the reactants in the above figure is ![]() Go,
not
Go,
not ![]() Go.
A small capital "G" is used to remind us that this diagram plots the free energy
of a pair of molecules as they react, not the free energy of a system that contains many
pairs of molecules undergoing collision. If we averaged the results of this calculation
over the entire array of molecules in the system, we would get the change in the free
energy of the system,
Go.
A small capital "G" is used to remind us that this diagram plots the free energy
of a pair of molecules as they react, not the free energy of a system that contains many
pairs of molecules undergoing collision. If we averaged the results of this calculation
over the entire array of molecules in the system, we would get the change in the free
energy of the system, ![]() Go.
Go.
Purists might also note that the symbol used to represent the activation energy is written with a capital "E". This is unfortunate, because it leads students to believe the activation energy is the change in the internal energy of the system, which is not quite true. Ea measures the change in the potential energy of a pair of molecules that is required to begin the process of converting a pair of reactant molecules into a pair of product molecules.
Catalysts and the Rates of Chemical Reactions
Aqueous solutions of hydrogen peroxide are stable until we add a small quantity of the I- ion, a piece of platinum metal, a few drops of blood, or a freshly cut slice of turnip, at which point the hydrogen peroxide rapidly decomposes.
2 H2O2(aq) ![]() 2 H2O(aq)
+ O2(g)
2 H2O(aq)
+ O2(g)
This reaction therefore provides the basis for understanding the effect of a catalyst on the rate of a chemical reaction. Four criteria must be satisfied in order for something to be classified as catalyst.
Catalysts increase the rate of reaction.
Catalysts are not consumed by the reaction.
A small quantity of catalyst should be able to affect the rate of reaction for a large amount of reactant.
Catalysts do not change the equilibrium constant for the reaction.
The first criterion provides the basis for defining a catalyst as something that increases the rate of a reaction. The second reflects the fact that anything consumed in the reaction is a reactant, not a catalyst. The third criterion is a consequence of the second; because catalysts are not consumed in the reaction, they can catalyze the reaction over and over again. The fourth criterion results from the fact that catalysts speed up the rates of the forward and reverse reactions equally, so the equilibrium constant for the reaction remains the same.
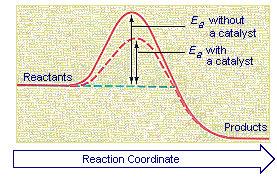
Catalysts increase the rates of reactions by providing a new mechanism that has a smaller activation energy, as shown in the figure below. A larger proportion of the collisions that occur between reactants now have enough energy to overcome the activation energy for the reaction. As a result, the rate of reaction increases.
To illustrate how a catalyst can decrease the activation energy for a reaction by providing another pathway for the reaction, let's look at the mechanism for the decomposition of hydrogen peroxide catalyzed by the I- ion. In the presence of this ion, the decomposition of H2O2 doesn't have to occur in a single step. It can occur in two steps, both of which are easier and therefore faster. In the first step, the I- ion is oxidized by H2O2 to form the hypoiodite ion, OI-.
H2O2(aq) + I-(aq)
![]() H2O(aq)
+ OI-(aq)
H2O(aq)
+ OI-(aq)
In the second step, the OI- ion is reduced to I- by H2O2.
OI-(aq) + H2O2(aq)
![]() H2O(aq)
+ O2(g) + I-(aq)
H2O(aq)
+ O2(g) + I-(aq)
Because there is no net change in the concentration of the I- ion as a result of these reactions, the I- ion satisfies the criteria for a catalyst. Because H2O2 and I- are both involved in the first step in this reaction, and the first step in this reaction is the rate-limiting step, the overall rate of reaction is first-order in both reagents.
Determining the Activation Energy of a Reaction
The rate of a reaction depends on the temperature at which it is run. As the temperature increases, the molecules move faster and therefore collide more frequently. The molecules also carry more kinetic energy. Thus, the proportion of collisions that can overcome the activation energy for the reaction increases with temperature.
The only way to explain the relationship between temperature and the rate of a reaction is to assume that the rate constant depends on the temperature at which the reaction is run. In 1889, Svante Arrhenius showed that the relationship between temperature and the rate constant for a reaction obeyed the following equation.
![]()
In this equation, k is the rate constant for the reaction, Z is a proportionality constant that varies from one reaction to another, Ea is the activation energy for the reaction, R is the ideal gas constant in joules per mole kelvin, and T is the temperature in kelvin.
The Arrhenius equation can be used to determine the activation energy for a reaction. We start by taking the natural logarithm of both sides of the equation.
![]()
We then rearrange this equation to fit the equation for a straight line.
y = mx + b

According to this equation, a plot of ln k versus 1/T should give a straight line with a slope of - Ea/R, as shown in the figure below.

| Practice Problem 11: Use the following data to determine the activation energy for the decomposition of HI: Temperature (K) Rate Constant (M/s) 573 2.91 x 10-6 673 8.38 x 10-4 773 7.65 x 10-2 |
By paying careful attention to the mathematics of logarithms, it is possible to derive another form of the Arrhenius equation that can be used to predict the effect of a change in temperature on the rate constant for a reaction.

| Practice Problem 12: Calculate the rate of decomposition of HI at 600°C. |
The Arrhenius equation can also be used to calculate what happens to the rate of a reaction when a catalyst lowers the activation energy.