You may be familiar with acid-base titrations that use phenolphthalein as the endpoint indicator. You might not have noticed, however, what happens when a solution that contains phenolphthalein in the presence of excess base is allowed to stand for a few minutes. Although the solution initially has a pink color, it gradually turns colorless as the phenolphthalein reacts with the OH- ion in a strongly basic solution.
The table below shows what happens to the concentration of phenolphthalein in a solution that was initially 0.005 M in phenolphthalein and 0.61 M in OH- ion. As you can see when these data are plotted in the graph below, the phenolphthalein concentration decreases by a factor of 10 over a period of about four minutes.
Experimental Data for the Reaction Between Phenolphthalein and Excess Base
| Concentration of Phenolphthalein (M) |
Time (s) | |
| 0.0050 | 0.0 | |
| 0.0045 | 10.5 | |
| 0.0040 | 22.3 | |
| 0.0035 | 35.7 | |
| 0.0030 | 51.1 | |
| 0.0025 | 69.3 | |
| 0.0020 | 91.6 | |
| 0.0015 | 120.4 | |
| 0.0010 | 160.9 | |
| 0.00050 | 230.3 | |
| 0.00025 | 299.6 | |
| 0.00015 | 350.7 | |
| 0.00010 | 391.2 |
Experiments such as the one that gave us the data in the above table are
classified as measurements of chemical kinetics (from a Greek stem meaning "to
move"). One of the goals of these experiments is to describe the rate of reaction![]() the rate at which the reactants
are transformed into the products of the reaction.
the rate at which the reactants
are transformed into the products of the reaction.
The term rate is often used to describe the change in a quantity
that occurs per unit of time. The rate of inflation, for example, is the change in the
average cost of a collection of standard items per year. The rate at which an object
travels through space is the distance traveled per unit of time, such as miles per hour or
kilometers per second. In chemical kinetics, the distance traveled is the change in the
concentration of one of the components of the reaction. The rate of a reaction is
therefore the change in the concentration of one of the reactants![]()
![]() (X)
(X)![]() that occurs during a given period of time
that occurs during a given period of time![]()
![]() t.
t.
![]()
| Practice Problem 1: Use the data in the above table to calculate the rate at which phenolphthalein reacts with the OH- ion during each of the following periods: (a) During the first time interval, when the phenolphthalein concentration falls from 0.0050 M to 0.0045 M. (b) During the second interval, when the concentration falls from 0.0045 M to 0.0040 M. (c) During the third interval, when the concentration falls from 0.0040 M to 0.0035 M. |
Instantaneous Rates of Reaction and the Rate Law for a Reaction
The rate of the reaction between phenolphthalein and the OH- ion isn't constant; it changes with time. Like most reactions, the rate of this reaction gradually decreases as the reactants are consumed. This means that the rate of reaction changes while it is being measured.
To minimize the error this introduces into our measurements, it seems
advisable to measure the rate of reaction over periods of time that are short compared
with the time it takes for the reaction to occur. We might try, for example, to measure
the infinitesimally small change in concentration![]() d(X)
d(X)![]() that occurs over an infinitesimally short period of time
that occurs over an infinitesimally short period of time![]() dt. The ratio of these
quantities is known as the instantaneous rate of reaction.
dt. The ratio of these
quantities is known as the instantaneous rate of reaction.
![]()
The instantaneous rate of reaction at any moment in time can be calculated from a graph of the concentration of the reactant (or product) versus time. The graph below shows how the rate of reaction for the decomposition of phenolphthalein can be calculated from a graph of concentration versus time. The rate of reaction at any moment in time is equal to the slope of a tangent drawn to this curve at that moment.
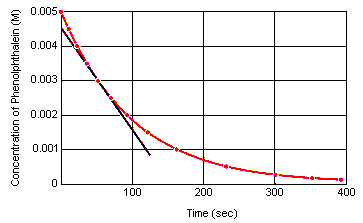
The instantaneous rate of reaction can be measured at any time between the moment at which the reactants are mixed and the reaction reaches equilibrium. Extrapolating these data back to the instant at which the reagents are mixed gives the initial instantaneous rate of reaction.
An interesting result is obtained when the instantaneous rate of reaction is calculated at various points along the curve in the graph in the previous section. The rate of reaction at every point on this curve is directly proportional to the concentration of phenolphthalein at that moment in time.
Rate = k(phenolphthalein)
Because this equation is an experimental law that describes the rate of the reaction, it is called the rate law for the reaction. The proportionality constant, k, is known as the rate constant.
| Practice Problem 2: Calculate the rate constant for the reaction between phenolphthalein and the OH- ion if the instantaneous rate of reaction is 2.5 x 10-5 mole per liter per second when the concentration of phenolphthalein is 0.0025 M. |
| Practice Problem 3: Use the rate constant for the reaction between phenolphthalein and the OH- ion to calculate the initial instantaneous rate of reaction for the experimental data listed in the preceding table. |
Different Ways of Expressing the Rate of Reaction
There is usually more than one way to measure the rate of a reaction. We can study the decomposition of hydrogen iodide, for example, by measuring the rate at which either H2 or I2 is formed in the following reaction or the rate at which HI is consumed.
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Experimentally we find that the rate at which I2 is formed is proportional to the square of the HI concentration at any moment in time.
![]()
What would happen if we studied the rate at which H2 is formed? The balanced equation suggests that H2 and I2 must be formed at exactly the same rate.
![]()
What would happen, however, if we studied the rate at which HI is consumed in this reaction? Because HI is consumed, the change in its concentration must be a negative number. By convention, the rate of a reaction is always reported as a positive number. We therefore have to change the sign before reporting the rate of reaction for a reactant that is consumed in the reaction.
![]()
The negative sign does two things. Mathematically, it converts a negative change in the concentration of HI into a positive rate. Physically, it reminds us that the concentration of the reactant decreases with time.
What is the relationship between the rate of reaction obtained by monitoring the formation of H2 or I2 and the rate obtained by watching HI disappear? The stoichiometry of the reaction says that two HI molecules are consumed for every molecule of H2 or I2 produced. This means that the rate of decomposition of HI is twice as fast as the rate at which H2 and I2 are formed. We can translate this relationship into a mathematical equation as follows.
![]()
As a result, the rate constant obtained from studying the rate at which H2 and I2 are formed in this reaction (k) is not the same as the rate constant obtained by monitoring the rate at which HI is consumed (k')
| Practice Problem 4: Calculate the rate at which HI disappears in the following reaction at the moment when I2 is being formed at a rate of 1.8 x 10-6 moles per liter per second: 2 HI(g) |
The Rate Law Versus the Stoichiometry of a Reaction
In the 1930s, Sir Christopher Ingold and coworkers at the University of London studied the kinetics of substitution reactions such as the following.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
They found that the rate of this reaction is proportional to the concentrations of both reactants.
Rate = k(CH3Br)(OH-)
When they ran a similar reaction on a slightly different starting material, they got similar products.
(CH3)3CBr(aq) + OH-(aq)
![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
But now the rate of reaction was proportional to the concentration of only one of the reactants.
Rate = k((CH3)3CBr)
These results illustrate an important point: The rate law for a reaction cannot be predicted from the stoichiometry of the reaction; it must be determined experimentally. Sometimes, the rate law is consistent with what we expect from the stoichiometry of the reaction.
2 HI(g) H2(g) + I2(g)
Rate = k(HI)2
Often, however, it is not.
| 2 N2O5(g) |
Rate = k(N2O5) |
Some reactions occur in a single step. The reaction in which a chlorine atom is transferred from ClNO2 to NO to form NO2 and ClNO is a good example of a one-step reaction.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
Other reactions occur by a series of individual steps. N2O5, for example, decomposes to NO2 and O2 by a three-step mechanism.
| Step 1: | N2O5 |
|
| Step 2: | NO2 + NO3 |
|
| Step 3: | NO + NO3 |
The steps in a reaction are classified in terms of molecularity, which describes the number of molecules consumed. When a single molecule is consumed, the step is called unimolecular. When two molecules are consumed, it is bimolecular.
| Practice Problem 5: Determine the molecularity of each step in the reaction by which N2O5 decomposes to NO2 and O2. |
Reactions can also be classified in terms of their order. The decomposition of N2O5 is a first-order reaction because the rate of reaction depends on the concentration of N2O5 raised to the first power.
Rate = k(N2O5)
The decomposition of HI is a second-order reaction because the rate of reaction depends on the concentration of HI raised to the second power.
Rate = k(HI)2
When the rate of a reaction depends on more than one reagent, we classify the reaction in terms of the order of each reagent.
| Practice Problem 6: Classify the order of the reaction between NO and O2 to form NO2: 2 NO(g) + O2(g) Assume the following rate law for this reaction: Rate = k(NO)2(O2) |
The difference between the molecularity and the order of a reaction is important. The molecularity of a reaction, or a step within a reaction, describes what happens on the molecular level. The order of a reaction describes what happens on the macroscopic scale. We determine the order of a reaction by watching the products of a reaction appear or the reactants disappear. The molecularity of the reaction is something we deduce to explain these experimental results.
Collision Theory Model of Chemical Reactions
The collision theory model of chemical reactions can be used to explain the observed rate laws for both one-step and multi-step reactions. This model assumes that the rate of any step in a reaction depends on the frequency of collisions between the particles involved in that step.
The figure below provides a basis for understanding the implications of the collision theory model for simple, one-step reactions, such as the following.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)

The kinetic molecular theory assumes that the number of collisions per second in a gas depends on the number of particles per liter. The rate at which NO2 and ClNO are formed in this reaction should therefore be directly proportional to the concentrations of both ClNO2 and NO.
Rate = k(ClNO2)(NO)
The collision theory model suggests that the rate of any step in a reaction is proportional to the concentrations of the reagents consumed in that step. The rate law for a one-step reaction should therefore agree with the stoichiometry of the reaction.
The following reaction, for example, occurs in a single step.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
When these molecules collide in the proper orientation, a pair of nonbonding electrons on the OH- ion can be donated to the carbon atom at the center of the CH3Br molecule, as shown in the figure below.
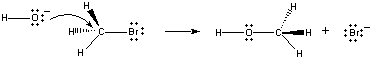
When this happens, a carbon-oxygen bond forms at the same time that the carbon-bromine bond is broken. The net result of this reaction is the substitution of an OH- ion for a Br - ion. Because the reaction occurs in a single step, which involves collisions between the two reactants, the rate of this reaction is proportional to the concentration of both reactants.
Rate = k(CH3Br)(OH-)
Not all reactions occur in a single step. The following reaction occurs in three steps, as shown in the figure below.
(CH3)3CBr(aq) + OH-(aq)
![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
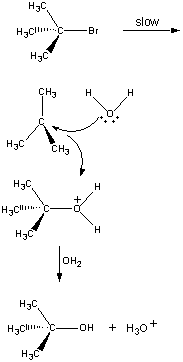
In the first step, the (CH3)3CBr molecule dissociates into a pair of ions.
| First step |
The positively charged (CH3)3C+ ion then reacts with water in a second step.
| Second step | 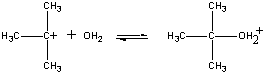 |
The product of this reaction then loses a proton to either the OH- ion or water in the final step.
| Third step | 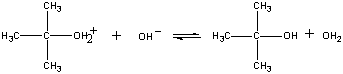 |
The second and third steps in this reaction are very much faster than first.
| (CH3)3CBr |
Slow step | |
| (CH3)3C+ + H2O |
Fast step | |
| (CH3)3COH2+ + OH-
|
Fast step |
The overall rate of reaction is therefore more or less equal to the rate of the first step. The first step is therefore called the rate-limiting step in this reaction because it literally limits the rate at which the products of the reaction can be formed. Because only one reagent is involved in the rate-limiting step, the overall rate of reaction is proportional to the concentration of only this reagent.
Rate = k((CH3)3CBr)
The rate law for this reaction therefore differs from what we would predict from the stoichiometry of the reaction. Although the reaction consumes both (CH3)3CBr and OH-, the rate of the reaction is only proportional to the concentration of (CH3)3CBr.
The rate laws for chemical reactions can be explained by the following general rules.
The rate of any step in a reaction is directly proportional to the concentrations of the reagents consumed in that step.
The overall rate law for a reaction is determined by the sequence of steps, or the mechanism, by which the reactants are converted into the products of the reaction.
The overall rate law for a reaction is dominated by the rate law for the slowest step in the reaction.