STATISTICAL ANALYSIS OF
MULTIPLE CHOICE EXAMS
Disraeli once said that there are three types of lies. In order of increasing severity, they are: "lies, damned lies, and statistics." This quotation has an inordinate attraction for many, regardless of its validity. There is nothing inherently wrong with statistics, however, if they are used by individuals who understand them.
The use of a multiple-choice format for hour exams at many institutions leads to a deluge of statistical data, which are often neglected or completely ignored. This section will introduce some of the terms encountered in the analysis of test results, so that these data may become more meaningful and therefore more useful.(1)
We might begin with definitions of measures of the mid-point of a normal,
Gaussian, or bell-shaped distribution of grades. The mode, or modal point, is the score obtained by the largest number of students. The median is the score obtained by the middle student in the group -- half the students
did better than the median, while half did worse. The mean (
) is the sum of the test scores divided by the number of students taking
the exam.
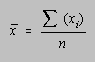
The mean is the quantity that was once called the average, before this term came to connotate "normal," and therefore became pejorative. The mean is simultaneously the most tedious of these quantities to calculate and the most representative measure of the mid-point of a test distribution.
The simplest measure of the distribution of scores around the mean is the range of scores, which is the difference between the highest and lowest scores, plus one.
Better measures of the distribution of scores are the variance and standard deviation. The variance (
2) is the sum of the squares of the deviations of the individual test scores
(xi) from the mean () divided by the number of scores (n). The standard deviation () is the square root of the variance.
Although the number of students enrolled in introductory chemistry courses often seems infinite, or at least transfinite, it is usually better to calculate the variance (s2) and standard deviation (s) in terms of the number of degrees of freedom available in their determination: n - 1.
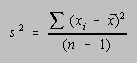
The standard deviation can be determined more rapidly if the variance (s2) is calculated using either of the following formulas.
Under ideal conditions, in which the distribution of scores is truly Gaussian,
34.13% of the scores would fall between the mean () and the mean plus one standard deviation ( + ), while another 34.13% would fall between and - . Thus, 68.26% of the scores in an ideal distribution would fall in the
range of ± . Another 13.59% of the scores would fall between one and two standard deviations
above the mean, or between one and two standard deviations below the mean.
Another 2.14% of the scores would fall between two and three standard deviations
either above or below the mean. A total of 99.72% of the scores would therefore
fall within a range of six standard deviations around the mean.
It should be noted that chemistry courses seldom give a truly Gaussian distribution of grades. Even in courses that enrolled as many as 1500 students, the author has never observed a distribution of grades that matched this ideal. Although the distribution of grades is seldom symmetric around the mean, it is often symmetric enough to justify the calculation of scaled scores.
An absolute or raw score on an exam does not indicate how a student's performance compares with that student's peers. Scaled scores are therefore calculated to unambiguously indicate the student's location within the distribution of scores. Two of the more popular scaled scores are the z- and T-scores. The z-score is equal to the number of standard deviations that a student's raw score falls either above or below the mean. For example, if a student obtains a raw score of 20 on an exam with a mean of 50 and a standard deviation of 15, the raw score is exactly two standard deviations below the mean, and the z-score would be -2.00. A raw score of 65 on the same exam would correspond to a z-score of 1.00.
T-scores transform the grade to a scale on which the mean has been arbitrarily
adjusted to 50 and the standard deviation has been scaled to exactly 10
points. T-scores may be calculated from the raw scores (xi), the mean (), and the standard deviation (), using the following equation:
Our student who was two standard deviations below the mean would have a T-score of 30, while the student who was one standard deviation above the mean would have a T-score of 60.
There are several advantages to z- or T-score data, which make these scales attractive. First, and foremost, the students know where they stand in the course at all times. Students who are told their raw scores, the mean, and the range of scores, cannot always interpret these data correctly. Some are overly confident; others are unduly afraid of failure. Using scaled scores, the students know where they stand relative to their peers. If the students are also informed of the typical distribution of grades, they can obtain an even better estimate of their standing in the course.
Scaled scores also allow the instructor to add any number of exam scores in the final analysis of grades without worrying about anomalous weighting of one or more of these exams. Regardless of the mean or standard deviation on a given exam, the z- or T-scores can be combined to produce a total that reflects the student's performance on each exam equally. If one wishes to drop the lowest exam score during the final analysis, it seems better to drop the lowest z- or T-score instead of the lowest exam score. Alternatively, if one wishes to weight one exam more heavily than another, all one need do is multiply the scaled score by an appropriate constant.
A third advantage of scaled scores is the ease -- and the accuracy -- with which exam grades can be prorated. If a student misses an exam for a legitimate reason, the instructor can prorate the exam by simply averaging the scaled scores on the student's other exams.
Rough Estimates of Test Reliability
A major advantage of the multiple-choice format is the ability to calculate data that pertain to the quality, or the reliability, of the exam -- the extent to which the exam discriminates between strong and weak students.
One of the simplest measures of the quality of an exam involves comparing the range of scores to the standard deviation. In general, as this ratio increases, the test becomes better at discriminating between students of differing levels of ability. For various reasons, the optimal ratio of the range to the standard deviation depends on the number of students enrolled in the course.
| Number of Students in the Course | Optimum Number of Standard Deviations in the Range |
| 25 | 3.9 |
| 50 | 4.5 |
| 100 | 5.0 |
| 500 | 6.1 |
| 1000 | 6.5 |
Pragmatically, we have found that ratios of 5 to 5.5 for 700-1000 student classes can be routinely obtained. Ratios that are significantly smaller would suggest that the exam does not discriminate between students to the extent desired.
The quality, or reliability, of an exam is also reflected by the standard error of measurement, which represents an attempt at estimating the error involved in measuring a particular student's grade with a particular exam. In theory, the observed score on an exam should lie within one standard error of measurement of the student's "true" score more than two-thirds of the time. As one might expect, the size of the standard error of measurement tends to reflect the number of points on the exam. Thus, one of the easiest ways to interpret this quantity is to compare the standard error to the range of exam scores. Ideally, the ratio of the range to the standard error should be on the order of 10:1, or larger. (In small classes, this ratio is virtually impossible to achieve.)
There are two points where relatively large values of the standard error of measurement become particularly meaningful: (1) when the mean is relatively low, and therefore the standard error is a significant fraction of the student's score, and (2) when the total of the standard error of measure-ment for the various exams in a course equals or exceeds the difference between the grade divisions for the course. Either situation would suggest that the grade assigned to an individual student is more arbitrary than we might like to admit.
Information about the quality of an exam is useless if this knowledge can't be translated into a means for improving subsequent exams. Fortunately, data can be calculated during the analysis of a multiple-choice exam that can provide hints as to how an exam can be improved.
There are two factors that affect the ability of an exam to discriminate between levels of student ability: (1) the quality of individual test items, and (2) the number of test items. The parameters that are useful in analyzing the quality of an individual test question are the proportion of the students who choose a particular answer to the question and the correlation between the probability of a student choosing this answer and the student's total score on the exam. These parameters are grouped together under the title item analysis.
Analysis of the proportion of students selecting each of the alternate answers to a question provides information on the difficulty of the question, as well as the extent to which answers that were meant to distract students actually function as distractors. These data do not indicate whether a question is good or bad. They do, however, allow one to determine whether questions that were designed to be relatively easy are indeed as trivial as desired, and whether questions that were designed to be difficult have met that goal, or become truly impossible. It has been suggested that questions that are answered correctly by more than 85%, or less than 25%, of the students are of questionable validity. Data on the frequency of selection of wrong answers are useful in revising questions for future use, since they provide a means for probing the attractive-ness of distractors that were included to catch the weaker students.
The correlation between the probability of a student choosing a particular answer to a question and the student's score on the exam can provide useful information on the ability of that question to discriminate between "strong" and "weak" students. In theory, the student who answers a given question correctly should have a tendency to perform better on the total exam than a student who answers the same question incorrectly. We therefore expect a positive correlation between the probability of a student getting a question right and the student's score on the exam. When the correlation coefficient for a correct answer is negative, something is drastically wrong with the question. Either the wrong answer has been entered into the grading key, or the question is grossly misleading. Conversely, we should expect a negative correlation between the probability of selecting a wrong answer and the total score on the exam. The correlation coefficient for wrong answers should therefore be negative and the occurrence of a positive correlation for a wrong answer is disconcerting.
Consider the following question used several years ago at Purdue.
Use the following data to answer questions 10-12.
OCl- + I-
OI- + Cl-
| [OCl-], M | 0.00250 | 0.00164 | 0.00122 | 0.000971 |
| time, s | 0 | 3 | 6 | 9 |
10. What is the rate constant (k) for this reaction?
The percentage of students selecting each of the five alternative answers and the correlation coefficients for these answers are summarized below.
The correct answer was d, and 60% of the students selected this choice. The correlation coefficient for this answer was 0.53, which suggested that there was a strong, positive correlation between the probability of a student getting this question right and doing well on the exam.
All of the incorrect answers were chosen by some of the students, which means they were adequate distractors. More importantly, the correlation coefficient was negative for all of the wrong answers. Finally, the correlation coefficients were large for the more popular wrong answers, which means that there was a strong, negative correlation between the probability of getting this question wrong and doing well on the exam.
Questions with correlation coefficients for correct answers between 0.00 and 0.19 are called inferior, or zero-order, discriminators and should be removed from future exams. Questions for which the coefficients are between 0.20 and 0.39 are good, or +1, discriminators. (Most of the questions written in our department fall within this range.) Questions for which the correlation is between 0.40 and 0.59 are very good, or +2, discriminators, and questions for which this correlation is above 0.60 -- the +3 discriminators -- should be bronzed.
The ideal exam would contain questions that lead to the selection of each alternative answer by a finite proportion of the student body, with a correlation between the correct answers and the total score on the order of 0.4 or better, and with negative correlations between the most popular wrong answers and the total score.
There are a number of statistical formulas for quantitatively estimating
the reliability of an exam. The Kuder-Richardson formula 20 (KR20), for example, calculates a reliability coefficient based on the number
of test items (k), the proportion of the responses to an item that are correct (p), the proportion of responses that are incorrect (q), and the variance (2).
This formula can't be used when multiple-choice questions involve partial
credit, and it requires a detailed item analysis. Of the numerous Kuder-Richardson
formulas, a second, known as formula 21, has attained some popularity. The KR-21 reliability coefficient is calculated from the number of test items (k), the mean (x), and the variance (2).
This formula has the advantage that item analysis data are not included in its calculation. Unfor-tunately, this formula severely underestimates the reliability of an exam unless all questions have approximately the same level of difficulty.
What is the significance of a KR-20 coefficient of 0.697? Before this question can be answered, we must note that the level of discrimination increases as the number of test questions increases, regardless of the ability of an individual test question to discriminate between good and poor students. Thus, the reliability coefficient for a 20-item test cannot be compared directly with the same coefficient for a 50-item test. Fortunately, the Spearman-Brown prophecy formula can be used to predict the reliability of an exam that is made n times longer from the reliability of the shorter exam and the value of n.
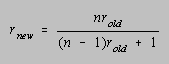
If the KR-20 coefficient for a 25-item test is 0.697, doubling the number of test questions should increase the reliability coefficient to 0.821, assuming that all items discriminate neither better or worse than the first 25.
To study the significance of the KR-20 coefficient, a set of 51 general chemistry exams used at Purdue University were examined. This set contained examples from all levels of our program, from remedial to our most advanced courses. In each case, the Spearman-Brown prophecy formula was used to predict what the coefficient would have been if the test had contained 50 questions. The mean value for the predicted KR-20 coefficient was 0.779, and the standard deviation was 0.076. It was interesting to note that the reliability coefficient was more susceptible to changes in instructor than to changes in the course to which the instructor was assigned.
It should be noted that the standard error of measurement, discussed previously,
can be calculated from the standard deviation for the exam () and the reliability coefficient (r) as follows.
Under certain circumstances, the statistical analysis discussed here begins to resemble a general chemistry student with an electronic calculator: Both provide answers to ten or more significant figures, all of which may be wrong. Under what conditions are we advised to accept these data with a grain of salt?
It appears that item analysis data for individual questions are valid, regardless of the number of questions, so long as the number of students taking the exam is sufficiently large, i.e., on the order of 100 or more. Attempts to apply this technique to study the differences between sections of 24 students in a multi-section course led to totally inconsistent results.
The assumptions behind the Spearman-Brown prophecy formula make calculations of reliability coefficients for exams that include only a limited number of test items worthless, regardless of how many students take the exam. These data are meaningful for exams that include a minimum of at least 15 test items.
There are at least three advantages to the use of a multiple-choice format for exams in courses that contain a reasonably large number of students. First, and foremost, we have found that careful consideration of the results of item analysis can lead to significant improvements in the quality of exams written by an instructor. Second, the multiple-choice format provides a consistency in grading that cannot be achieved when exams are graded by hand. Third, the use of the multiple-choice format for at least a portion of each exam frees teaching assistants and faculty for more pleasant, as well as more important tasks, than grading exams.
1. Taken in part from a paper published in the Journal of Chemical Education, 1980, 57, 188-190.
Test Question Bank Homepage