Equilibrium Expressions
Equilibrium Constant Expressions
Reactions don't stop when they come to equilibrium. But the
forward and reverse reactions are in balance at equilibrium, so
there is no net change in the concentrations of the reactants or
products, and the reaction appears to stop on the macroscopic
scale. Chemical equilibrium is an example of a dynamic
balance between opposing forces![]() the forward and reverse reactions
the forward and reverse reactions
![]() not a
static balance.
not a
static balance.
Let's look at the logical consequences of the assumption that the reaction between ClNO2 and NO eventually reaches equilibrium.
| ClNO2(g) | + | NO(g) | NO2(g) | + | ClNO(g) |
The rates of the forward and reverse reactions are the same when this system is at equilibrium.
| At equilibrium: | rateforward | = | ratereverse |
Substituting the rate laws for the forward and reverse reactions into this equality gives the following result.
| At equilibrium: | kf(ClNO2)(NO) | = | kr(NO2)(ClNO) |
But this equation is only valid when the system is at equilibrium, so we should replace the (ClNO2), (NO), (NO2), and (ClNO) terms with symbols that indicate that the reaction is at equilibrium. By convention, we use square brackets for this purpose. The equation describing the balance between the forward and reverse reactions when the system is at equilibrium should therefore be written as follows.
| At equilibrium: | kf[ClNO2][NO] | = | kr[NO2][ClNO] |
Rearranging this equation gives the following result.

Since kf and kr are constants, the ratio of kf divided by kr must also be a constant. This ratio is the equilibrium constant for the reaction, Kc. The ratio of the concentrations of the reactants and products is known as the equilibrium constant expression.
 |
|||
No matter what combination of concentrations of reactants and products we start with, the reaction will reach equilibrium when the ratio of the concentrations defined by the equilibrium constant expression is equal to the equilibrium constant for the reaction. We can start with a lot of ClNO2 and very little NO, or a lot of NO and very little ClNO2. It doesn't matter. When the reaction reaches equilibrium, the relationship between the concentrations of the reactants and products described by the equilibrium constant expression will always be the same. At 25oC, this reaction always reaches equilibrium when the ratio of these concentrations is 1.3 x 104.
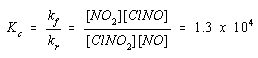
The procedure used in this section to derive the equilibrium constant expression only works with reactions that occur in a single step, such as the transfer of a chlorine atom from ClNO2 to NO. Many reactions take a number of steps to convert reactants into products. But any reaction that reaches equilibrium, no matter how simple or complex, has an equilibrium constant expression that satisfies the rules in the following section.
Rules for Writing Equilibrium Constant Expressions
| Practice Problem 1: Write equilibrium constant expressions for the following reactions.
|
Gas-phase reactions were chosen for this introduction to kinetics and equilibrium because they are among the simplest chemical reactions. Some might question, however, why the equilibrium constant expressions in the preceding exercise are expressed in terms of the concentrations of the gases in units of moles per liter.
Units of concentration were used to emphasize the relationship between chemical equilibria and the rates of chemical reactions, which are reported in terms of the concentrations of the reactants and products. This choice of units is indicated by adding a subscript "c" to the symbols for the equilibrium constants, to show that they were calculated from the concentrations of the components of the reaction.
Altering or Combining Equilibrium Reactions
What happens to the magnitude of the equilibrium constant for a reaction when we turn the equation around? Consider the following reaction, for example.
| ClNO2(g) | + | NO(g) | NO2(g) | + | ClNO(g) |
The equilibrium constant expression for this equation is written as follows.
Because this is a reversible reaction, it can also be represented by an equation written in the opposite direction.
| NO2(g) | + | ClNO(g) | ClNO2(g) | + | NO(g) |
The equilibrium constant expression is now written as follows.
 |
Each of these equilibrium constant expressions is the inverse of the other. We can therefore calculate Kc´ by dividing Kc into 1.
We can also calculate equilibrium constants by combining two or more reactions for which the value of Kc is known. Assume, for example, that we know the equilibrium constants for the following gas-phase reactions at 200oC.
| N2(g) | + | O2(g) | 2 NO(g) | Kc1 = 2.3 x 10-19 | ||
| 2 NO(g) | + | O2(g) | 2 NO2(g) | Kc2 = 3 x 106 |
We can combine these reactions to obtain an overall equation for the reaction between N2 and O2 to form NO2.
| N2(g) | + | O2(g) | |||
| + | + | O2(g) | 2 NO2(g) | ||
| ______________________________________________________________ | |||||
| N2(g) | + | 2 O2(g) | 2 NO2(g) | ||
It is easy to show that the equilibrium constant expression for the overall reaction is equal to the product of the equilibrium constant expressions for the two steps in this reaction.
 |
The equilibrium constant for the overall reaction is therefore equal to the product of the equilibrium constants for the individual steps.
Kc = Kc1 x Kc2 = (2.3 x 10-19)(3 x 106) = 7 x 10-13
Reaction Quotients: A Way to Decide Whether a Reaction is at Equilibrium
We have a model that describes what happens when a reaction
reaches equilibrium: At the molecular level, the rate of the
forward reaction is equal to the rate of the reverse reaction.
Since the reaction proceeds in both directions at the same rate,
there is no apparent change in the concentrations of the
reactants or the products on the macroscopic scale ![]() the level of
objects visible to the naked eye. This model can also be used to
predict the direction in which a reaction has to shift to reach
equilibrium.
the level of
objects visible to the naked eye. This model can also be used to
predict the direction in which a reaction has to shift to reach
equilibrium.
If the concentrations of the reactants are too large for the reaction to be at equilibrium, the rate of the forward reaction will be faster than the reverse reaction, and some of the reactants will be converted into products until equilibrium is achieved. Conversely, if the concentrations of the reactants are too small, the rate of the reverse reaction will exceed that of the forward reaction, and the reaction will convert some of the excess products back into reactants until the system reaches equilibrium.
We can determine the direction in which a reaction has to shift to reach equilibrium by calculating the reaction quotient (Qc) for the reaction. The reaction quotient is defined as the product of the concentrations of the products of the reaction divided by the product of the concentration of the reactants at any moment in time.
To illustrate how the reaction quotient is used, let's consider the following gas-phase reaction.
| H2(g) | + | I2(g) | 2 HI(g) |
The equilibrium constant expression for this reaction is written as follows.
 |
By analogy, we can write the expression for the reaction quotient as follows.
Qc can take on any value between zero and infinity. If the system contains a great deal of HI and very little H2 and I2, the reaction quotient is very large. If the system contains relatively little HI and a great deal of H2 and I2, the reaction quotient is very small.
At any moment in time, there are three possibilities.
1. Qc is smaller than Kc. The system contains too much reactant and not enough product to be at equilibrium. The value of Qc must increase in order for the reaction to reach equilibrium. Thus, the reaction has to convert some of the reactants into products to come to equilibrium.
2. Qc is equal to Kc. If this is true, then the reaction is at equilibrium.
3. Qc is larger than Kc. The system contains too much product and not enough reactant to be at equilibrium. The value of Qc must become smaller before the reaction can come to equilibrium. Thus, the reaction must convert some of the products into reactants to reach equilibrium.
| Practice Problem 2: Assume that the concentrations of H2, I2, and HI can be measured for the following reaction at any moment in time. H2(g) + I2(g)
For each of the following sets of concentrations, determine whether the reaction is at equilibrium. If it isn't, decide in which direction it must go to reach equilibrium. (a) (H2) = (I2) = (HI) = 0.010 M (b) (HI) = 0.30 M; (H2) = 0.01 M; (I2) = 0.15 M (c) (H2) = (HI) = 0.10 M; (I2) = 0.0010 M |
Changes in Concentration that Occur as a Reaction Comes to Equilibrium
The relative size of Qc and Kc for a reaction tells us whether the reaction is at equilibrium at any moment in time. If it isn't, the relative size of Qc and Kc tell us the direction in which the reaction must shift to reach equilibrium. Now we need a way of predicting how far the reaction has to go to reach equilibrium. Suppose that you are faced with the following problem.
Phosphorus pentachloride decomposes to phosphorus
trichloride and chlorine when heated.
The equilibrium constant for this reaction is 0.030 at 250oC. Assuming that the initial concentration of PCl5 is 0.100 moles per liter and there is no PCl3 or Cl2 in the system when we start, let's calculate the concentrations of PCl5, PCl3, and Cl2 at equilibrium. |
The first step toward solving this problem involves organizing
the information so that it provides clues as to how to proceed.
The problem contains four chunks of information: (1) a balanced
equation, (2) an equilibrium constant for the reaction, (3) a
description of the initial conditions, and (4) an indication of
the goal of the calculation ![]() the equilibrium concentrations of the
three components of the reaction.
the equilibrium concentrations of the
three components of the reaction.
The following format offers a useful way to summarize this information.
|
We start with the balanced equation and the equilibrium constant for the reaction and then add what we know about the initial and equilibrium concentrations of the various components of the reaction. Initially, the flask contains 0.100 moles per liter of PCl5 and no PCl3 or Cl2. Our goal is to calculate the equilibrium concentrations of these three substances.
Before we do anything else, we have to decide whether the reaction is at equilibrium. We can do this by comparing the reaction quotient for the initial conditions with the equilibrium constant for the reaction.
Although the equilibrium constant is small (Kc = 3.0 x 10-2), the reaction quotient is even smaller (Qc = 0). The only way for this reaction to get to equilibrium is for some of the PCl5 to decompose into PCl3 and Cl2.
Since the reaction isn't at equilibrium, one thing is sure![]() the
concentrations of PCl5, PCl3, and Cl2
will all change as the reaction comes to equilibrium. Because the
reaction has to shift to the right to reach equilibrium, the PCl5
concentration will become smaller, while the PCl3 and
Cl2 concentration will become larger.
the
concentrations of PCl5, PCl3, and Cl2
will all change as the reaction comes to equilibrium. Because the
reaction has to shift to the right to reach equilibrium, the PCl5
concentration will become smaller, while the PCl3 and
Cl2 concentration will become larger.
At first glance, this problem appears to have three unknowns: the equilibrium concentrations of PCl5, PCl3, and Cl2. Because it is difficult to solve a problem in three unknowns, we should look for relationships that can reduce the problem's complexity. One way of achieving this goal is to look at the relationship between the changes that occur in the concentrations of PCl5, PCl3, and Cl2 as the reaction approaches equilibrium.
| Practice Problem 3: Calculate the increase in the PCl3 and Cl2 concentrations that occur as the following reaction comes to equilibrium if the concentration of PCl5 decreases by 0.042 moles per liter. PCl5(g) |
There is a simple relationship between the change in the concentrations of the three components of the reaction as it comes to equilibrium because of the stoichiometry of the reaction.
It would be useful to have a symbol to represent the change that occurs in the concentration of one of the components of a reaction as it goes from the initial conditions to equilibrium. A state function is a property of a system whose value only depends on the state of the system. The change in the value of a state function is defined by the following equation.
![]() X = Xfinal - Xinitial
X = Xfinal - Xinitial
We can extend this argument to discussions of chemical
reactions that come to equilibrium by defining ![]() (X)
as the magnitude of the change that occurs in the concentration
of X as the reaction comes to equilibrium. We can define
(X)
as the magnitude of the change that occurs in the concentration
of X as the reaction comes to equilibrium. We can define
![]() (PCl5),
for example, as the magnitude of the change in the concentration
of PCl5 that occurs as this compound decomposes to
form PCl3 and Cl2.
(PCl5),
for example, as the magnitude of the change in the concentration
of PCl5 that occurs as this compound decomposes to
form PCl3 and Cl2.
| = | (PCl5) | - | [PCl5] | ||
| PCl5
consumed as the reaction comes to equilibrium |
initial concentration |
concentration at equilibrium |
Rearranging this equation, we find that the concentration of PCl5 at equilibrium is equal to the initial concentration of PCl5 minus the amount of PCl5 consumed as the reaction comes to equilibrium.
| [PCl5] | = | (PCl5) | - | ||
| concentration at equilibrium |
initial concentration |
PCl5
consumed as the reaction comes to equilibrium |
We can then define ![]() (PCl3) and
(PCl3) and ![]() (Cl2)
as the changes that occur in the PCl3 and Cl2
concentrations as the reaction comes to equilibrium. The
concentrations of both these substances at equilibrium will be
larger than their initial concentrations.
(Cl2)
as the changes that occur in the PCl3 and Cl2
concentrations as the reaction comes to equilibrium. The
concentrations of both these substances at equilibrium will be
larger than their initial concentrations.
| [PCl3] | = | (PCl3) | + | ||
| [Cl2] | = | (Cl2) | + |
The magnitude of the changes in the concentrations of these three substances as the reaction comes to equilibrium would be the same. Because of the 1:1:1 stoichiometry of the reaction, the magnitude of the change in the concentration of PCl5 as the reaction comes to equilibrium is equal to the magnitude of the change in the concentrations of PCl3 and Cl2.
![]() (PCl5) =
(PCl5) = ![]() (PCl3)
=
(PCl3)
= ![]() (Cl2)
(Cl2)
We can therefore rewrite the equations that define the
equilibrium concentrations of PCl5, PCl3,
and Cl2 in terms of a single unknown: ![]() C.
C.
[PCl5] = (PCl5) - ![]() C
C
[PCl3] = (PCl3) + ![]() C
C
[Cl2] = (Cl2) + ![]() C
C
Substituting what we know about the initial concentrations of PCl5, PCl3, and Cl2 into these equations gives the following result.
[PCl5] = 0.100 - ![]() C
C
[PCl3] = [Cl2] = 0 + ![]() C
C
We can now summarize what we know about this reaction as follows.
|
We now have only one unknown ![]()
![]() C
C ![]() and we need only one equation to solve for
one unknown. The obvious equation to turn to is the equilibrium
constant expression for this reaction.
and we need only one equation to solve for
one unknown. The obvious equation to turn to is the equilibrium
constant expression for this reaction.
Substituting what we know about the equilibrium concentrations of PCl5, PCl3, and Cl2 into this equation gives the following result.
This equation can be expanded and then rearranged to give a quadratic equation
![]() C2 + 0.030
C2 + 0.030 ![]() C - 0.0030 =
0
C - 0.0030 =
0
which can be solved with the quadratic formula.
 |
![]() C = 0.042 or -0.072
C = 0.042 or -0.072
Although two answers come out of this calculation, only the positive root makes any physical sense, because we can't have a negative concentration. Thus, the magnitude of the change in the concentrations of PCl5, PCl3, and Cl2 as this reaction comes to equilibrium is 0.042 moles per liter.
![]() C= 0.042 M
C= 0.042 M
Plugging this value of back into the equations that define the equilibrium concentrations of PCl5, PCl3, and Cl2 gives the following results.
[PCl5] = 0.100 - 0.042 = 0.058 M
[PCl3] = [Cl2] = 0 + 0.042 = 0.042 M
In other words, slightly less than half of the PCl5 present initially decomposes into PCl3 and Cl2 when this reaction comes to equilibrium.
To check whether the results of this calculation represent legitimate values for the equilibrium concentrations of the three components of this reaction, we can substitute these values into the equilibrium constant expression.

These results must be legitimate because the equilibrium constant calculated from these concentrations is equal to the value of Kc given in the problem, within experimental error.
| Practice Problem 4: Assume the following initial concentrations: (PCl5) = 0.100 M and (Cl2) = 0.020 M. Calculate the equilibrium concentrations of PCl5, PCl3, and Cl2 if the equilibrium constant for the decomposition of PCl5 is 0.030. |
Hidden Assumptions that Make Equilibrium Calculations Easier
Suppose that you were asked to solve a slightly difficult problem.
|
The first step in this problem involves building a representation of the information in the problem.
|
We then compare the reaction quotient for the initial conditions with the equilibrium constant for the reaction.
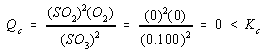 |
Because the initial concentrations of SO2 and O2 are zero, the reaction has to shift to the right to reach equilibrium. As might be expected, some of the SO3 has to decompose to SO2 and O2.
The stoichiometry of this reaction is more complex than the reaction in the previous section, but the changes in the concentrations of the three components of the reaction are still related. For every two moles of SO3 that decompose we get two moles of SO2 and one mole of O2, as shown in the figure below. We can incorporate this relationship into the format we used earlier by using the balanced equation for the reaction as a guide.
 |
The signs of the ![]() C terms in this problem are determined
by the fact that the reaction has to shift from left to right to
reach equilibrium. The coefficients in the
C terms in this problem are determined
by the fact that the reaction has to shift from left to right to
reach equilibrium. The coefficients in the ![]() C terms
mirror the coefficients in the balanced equation for the
reaction. Because twice as many moles of SO2 are
produced as moles of O2, the change in the
concentration of SO2 as the reaction comes to
equilibrium must be twice as large as the change in the
concentration of O2. Because two moles of SO3
are consumed for every mole of O2 produced, the change
in the SO3 concentration must be twice as large as the
change in the concentration of O2.
C terms
mirror the coefficients in the balanced equation for the
reaction. Because twice as many moles of SO2 are
produced as moles of O2, the change in the
concentration of SO2 as the reaction comes to
equilibrium must be twice as large as the change in the
concentration of O2. Because two moles of SO3
are consumed for every mole of O2 produced, the change
in the SO3 concentration must be twice as large as the
change in the concentration of O2.
| 2 SO3(g) | 2 SO2(g) | + | O2(g) | Kc = 1.6 x 10-10 | |||||
| Initial: | 0.100 M | 0 | 0 | ||||||
| Change: | -2 |
+2 |
+ |
||||||
| Equilibrium: | 0.100 - 2 |
2 |
Substituting what we know about the problem into the equilibrium constant expression for the reaction gives the following equation.

This equation is a bit more of a challenge to expand, but it can be rearranged to give the following cubic equation.
4![]() C3 - 6.4 x 10-10
C3 - 6.4 x 10-10![]() C2
+ 6.4 x 10-11
C2
+ 6.4 x 10-11![]() C - 1.6 x 10-12 = 0
C - 1.6 x 10-12 = 0
Solving cubic equations is difficult, however. This problem is therefore an example of a family of problems that are difficult, if not impossible, to solve exactly. These problems are solved with a general strategy that consists of making an assumption or approximation that turns them into simpler problems. The following general rules will guide our discussion of methods of approximation.
| RULES FOR USING APPROXIMATION
METHODS 1. There is nothing wrong with making an assumption. 2. There are two cardinal sins: (a) Forgetting what assumptions were made. (b) Forgetting to check whether the assumptions are valid. |
What assumption can be made to simplify this problem? Let's go back to the first thing we did after building a representation for the problem. We started our calculation by comparing the reaction quotient for the initial concentrations with the equilibrium constant for the reaction.
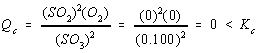
We then concluded that the reaction quotient (Qc = 0) was smaller than the equilibrium constant (Kc = 1.6 x 10-10) and decided that some of the SO3 would have to decompose in order for this reaction to come to equilibrium.
But what about the relative sizes of the reaction quotient and
the equilibrium constant for the reaction? The initial values of Qc
and Kc are both relatively small,
which means that the initial conditions are reasonably close to
equilibrium, as shown in the figure below. As a result, the
reaction does not have far to go to reach equilibrium. It is
therefore reasonable to assume that ![]() C is
relatively small in this problem.
C is
relatively small in this problem.
 |
It is essential to understand the nature of the assumption
being made. We are not assuming that ![]() C is
zero. If we did that, all of the unknowns would disappear from
the equation! We are only assuming that
C is
zero. If we did that, all of the unknowns would disappear from
the equation! We are only assuming that ![]() C is
small. So small compared with the initial concentration of SO3
that it doesn't make a significant difference when 2
C is
small. So small compared with the initial concentration of SO3
that it doesn't make a significant difference when 2![]() C is
subtracted from this number. We can write this assumption as
follows.
C is
subtracted from this number. We can write this assumption as
follows.
0.100 - 2 ![]() C
C ![]() 0.100
0.100
Let's now go back to the equation we are trying to solve.
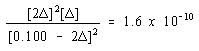
By making the assumption that 2![]() C is
very much smaller than 0.100, we can replace this equation with
the following approximate equation.
C is
very much smaller than 0.100, we can replace this equation with
the following approximate equation.
![]()
Expanding this gives an equation that is much easier to solve for .
4![]() C3
C3 ![]() 1.6 x 10-12
1.6 x 10-12
![]() C
C ![]() 7.4 x 10-5 M
7.4 x 10-5 M
Before we can go any further, we have to check our assumption
that 2![]() C
is so small compared with 0.100 that it doesn't make a
significant difference when it is subtracted from this number. Is
this assumption valid? Is 2
C
is so small compared with 0.100 that it doesn't make a
significant difference when it is subtracted from this number. Is
this assumption valid? Is 2![]() C small enough compared with 0.100 to
be ignored?
C small enough compared with 0.100 to
be ignored?
0.100 - 2(0.000074)![]() 0.100
0.100
Yes, 2![]() C
is an order of magnitude smaller than the experimental error
involved in the measurement of the initial concentration of SO3.
C
is an order of magnitude smaller than the experimental error
involved in the measurement of the initial concentration of SO3.
We can therefore use this approximate value of ![]() C to
calculate the equilibrium concentrations of SO3, SO2,
and O2.
C to
calculate the equilibrium concentrations of SO3, SO2,
and O2.
[SO3] = 0.100 - 2![]() C
C ![]() 0.100 M
0.100 M
[SO2] = 2![]() C
C ![]() 1.5 x 10-4 M
1.5 x 10-4 M
[O2] = ![]() C
C ![]() 7.4 x 10-5 M
7.4 x 10-5 M
The equilibrium between SO3 and mixtures of SO2 and O2 therefore strongly favors SO3, not SO2.
We can check the results of our calculation by substituting these results into the equilibrium constant expression for the reaction.

The value of the equilibrium constant that comes out of this
calculation agrees with the value given in the problem, within
experimental error. Our assumption that 2![]() C is
negligibly small compared with the initial concentration of SO3
is therefore valid, and we can feel confident in the answers it
provides.
C is
negligibly small compared with the initial concentration of SO3
is therefore valid, and we can feel confident in the answers it
provides.
A Rule of Thumb for Testing the Validity of Assumptions
There was no doubt about the validity of the assumption that ![]() C was small
compared with the initial concentration of SO3 in the
preceding section. The value of
C was small
compared with the initial concentration of SO3 in the
preceding section. The value of ![]() C was so small that 2
C was so small that 2![]() C was an
order of magnitude smaller than the experimental error involved
in measuring the initial concentration of SO3.
C was an
order of magnitude smaller than the experimental error involved
in measuring the initial concentration of SO3.
In general, we can get some idea of whether ![]() C might be
small enough to be ignored by comparing the initial reaction
quotient with the equilibrium constant for the reaction. If Qc
and Kc are both much smaller than 1,
or both much larger than 1, the reaction doesn't have very far to
go to reach equilibrium, and the assumption that
C might be
small enough to be ignored by comparing the initial reaction
quotient with the equilibrium constant for the reaction. If Qc
and Kc are both much smaller than 1,
or both much larger than 1, the reaction doesn't have very far to
go to reach equilibrium, and the assumption that ![]() C is small
enough to be ignored is probably legitimate.
C is small
enough to be ignored is probably legitimate.
This raises an interesting question: How
do we decide whether it is valid to assume that is small enough
to be ignored? The answer to this question depends on how much
error we are willing to let into our calculation before we no
longer trust the results. As a rule of thumb, chemists typically
assume that ![]() C is negligibly small as long as what
is added to or subtracted from the initial concentrations of the
reactants or products is less than 5% of the initial
concentration. The best way to decide whether the assumption
meets this rule of thumb in a particular calculation is to try it
and see if it works.
C is negligibly small as long as what
is added to or subtracted from the initial concentrations of the
reactants or products is less than 5% of the initial
concentration. The best way to decide whether the assumption
meets this rule of thumb in a particular calculation is to try it
and see if it works.
| Practice Problem 5: Ammonia is made from nitrogen and hydrogen by the following reversible reaction. N2(g) + 3 H2(g) Assume that the initial concentration of N2 is 0.050 moles per liter and the initial concentration of H2 is 0.100 moles per liter. Calculate the equilibrium concentrations of the three components of this reaction at 500oC if the equilibrium constant for the reaction at this temperature is 0.040. |
What Do We Do When the Approximation Fails?
It is easy to envision a problem in which the assumption that ![]() C is small
compared with the initial concentrations can't possibly be valid.
All we have to do is construct a problem in which there is a
large difference between the values of Qc
for the initial concentrations and Kc
for the reaction at equilibrium. Consider the following problem,
for example.
C is small
compared with the initial concentrations can't possibly be valid.
All we have to do is construct a problem in which there is a
large difference between the values of Qc
for the initial concentrations and Kc
for the reaction at equilibrium. Consider the following problem,
for example.
|
We start, once again, by representing the information in the problem as follows.
|
The first step is always the same: Compare the initial value of the reaction quotient with the equilibrium constant.

The relationship between the initial reaction quotient (Qc = 0) and the equilibrium constant (Kc = 3 x 106) tells us something we may already have suspected, the reaction must shift to the right to reach equilibrium.
Some might ask: "Why calculate the initial value of the reaction quotient for this reaction? Isn't it obvious that the reaction has to shift to the right to produce at least some NO2?" Yes, it is. But calculating the value of Qc for the reaction does more than tell us in which direction it has to shift to reach equilibrium. It also gives us an indication of how far the reaction has to go to reach equilibrium.
In this case, Qc is so very much smaller than Kc for the reaction that we have to conclude that the initial conditions are very far from equilibrium. It would therefore be a mistake to assume that is small.
We can't assume that is negligibly small in this problem, but we can redefine the problem so that this assumption becomes valid. The key to achieving this goal is to remember the conditions under which we can assume that is small enough to be ignored. This assumption is only valid when Qc is of the same order of magnitude as Kc. (When Qc and Kc are both much larger than 1 or much smaller than 1.) We can solve problems for which Qc isn't close to Kc by redefining the initial conditions so that Qc becomes close to Kc (see figure below).
 |
To show how this can be done, let's return to the problem given in this section.
The equilibrium constant for the reaction between NO and O2 to form NO2 is much larger than 1 (Kc = 3 x 106). This means that the equilibrium favors the products of the reaction. The best way to handle this problem is to drive the reaction as far as possible to the right, and then let it come back to equilibrium. Let's therefore define an intermediate set of conditions that correspond to what would happen if we push the reaction as far as possible to the right.
|
We can see where this gets us by calculating the reaction quotient for the intermediate conditions.
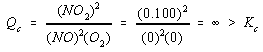
The reaction quotient is now larger than the equilibrium constant, and the reaction has to shift back to the left to reach equilibrium. Some of the NO2 must now decompose to form NO and O2.The relationship between the changes in the concentrations of the three components of this reaction is determined by the stoichiometry of the reaction, as shown in the figure below.
|
![]() (NO2) is twice as large as
(NO2) is twice as large as ![]() (O2).
(O2).
| 2 NO(g) | + | O2(g) | 2 NO2(g) | Kc = 3 x 106 | ||||
| Intermediate: | 0 | 0 | 0.100 M | |||||
| Change: | +2 |
+ |
-2 |
|||||
| Equilibrium: | 2 |
0.100 - 2 |
We now substitute what we know about the reaction into the equilibrium constant expression.

Because the reaction quotient for the intermediate conditions
and the equilibrium constant are both relatively large, we can
assume that the reaction doesn't have very far to go to reach
equilibrium. In other words, we assume that 2 ![]() C is
small compared with the intermediate concentration of NO2
and derive the following approximate equation.
C is
small compared with the intermediate concentration of NO2
and derive the following approximate equation.

We then solve this equation for an approximate value of ![]() C.
C.
![]()
We now check our assumption that 2 ![]() C is
small enough compared with the intermediate concentration of NO2
to be ignored.
C is
small enough compared with the intermediate concentration of NO2
to be ignored.
![]()
The value of 2![]() C is less than 2% of the intermediate
concentration of NO2, which means that it can be
legitimately ignored in this calculation.
C is less than 2% of the intermediate
concentration of NO2, which means that it can be
legitimately ignored in this calculation.
Since the approximation is valid, we can use the new value of to calculate the equilibrium concentrations of NO, NO2, and O2.
| [NO2] = 0.100 - 2 |
| [NO] = 2 |
| [O2] = |
The results of this calculation provide insight into the chemistry of the pollutants formed by an internal combustion engine. When a mixture of gasoline and air is burned, the N2 and O2 in air react to form NO, which can then react with oxygen to form NO2.
| N2(g) | + | O2(g) | 2 NO(g) | ||
| 2 NO(g) | + | O2(g) | 2 NO2(g) |
Although the product of these reactions is often described as
NOx ![]() to indicate that it is a mixture of NO and NO2
to indicate that it is a mixture of NO and NO2
![]() this
calculation suggests that the dominant product of the reaction
would be NO2, if this reaction comes to equilibrium.
this
calculation suggests that the dominant product of the reaction
would be NO2, if this reaction comes to equilibrium.
We can check our calculations by substituting these concentrations back into the equilibrium constant expression.

Once again, we can accept the validity of the assumption we had to make to get these equilibrium concentrations because the value of the equilibrium constant that comes out of this calculation agrees with the value of Kc given in the problem, within experimental error.
In general, the assumption that ![]() C is small compared with the
initial concentrations of the reactants or products works best
under the following conditions.
C is small compared with the
initial concentrations of the reactants or products works best
under the following conditions.
1. When Kc << 1 and we approach equilibrium from left to right. (We start with excess reactants and form some products.)
2. When Kc >> 1 and we approach equilibrium from right to left. (We start with excess products and form some reactants.)
Equilibria Expressed in Partial Pressures
Chemists usually study gas-phase equilibria by following the partial pressures of the gases in the reaction. We can understand why this is possible by rearranging the ideal gas equation to give the following relationship between the pressure of a gas and its concentration in moles per liter.
![]()
We can therefore characterize the following reaction
| N2(g) | + | 3 H2(g) | 2 NH3(g) |
with an equilibrium constant defined in terms of units of concentration

or an equilibrium constant defined in terms of partial pressures.
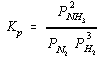
What is the relationship between Kp and Kc for a gas-phase reaction? According to the rearranged version of the ideal gas equation, the pressure of a gas is equal to the concentration of the gas times the product of the ideal gas constant and the temperature in units of kelvin.
![]()
We can therefore calculate the value of Kp for a reaction by multiplying each of the terms in the Kc expression by RT.
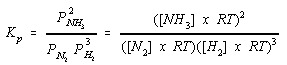
Collecting terms in this example gives the following result.
Kp = Kc x (RT)-2
In general, the value of Kp for a reaction can be calculated from Kc with the following equation.
![]()
In this equation, ![]() n is the difference between the number of moles
of products and the number of moles of reactants in the balanced
equation.
n is the difference between the number of moles
of products and the number of moles of reactants in the balanced
equation.
| Practice Problem 6: Calculate the value of Kp for the following reaction at 500oC if the value of Kc for the reaction at this temperature is 0.040. N2(g) + 3 H2(g) |
The techniques for working problems using Kp expressions are the same as those described for Kc problems, except that partial pressures are used instead of concentrations to represent the amounts of starting materials and products that are present both initially and at equilibrium.
The Effect of Temperature on a Chemical Reaction
If the equilibrium constant is really constant, why do we have to worry about the temperature of the reaction?
The answer is simple. Both Kc and Kp for a reaction are constants at a given temperature, but they can change with temperature. Consider the equilibrium between NO2 and its dimer, N2O4, for example.
| 2 NO2(g) | N2O4(g) |
The figure below shows the effect of temperature on this equilibrium. When we cool a sealed tube containing NO2 in a dry-ice/acetone bath at -78oC, the intensity of the brown color of NO2 gas decreases significantly. If we warm the tube in a hot-water bath, the brown color becomes more intense than it was at room temperature.

The equilibrium constant for this reaction changes with temperature, as shown in the table below. At low temperatures, the equilibrium favors the dimer, N2O4. At high temperatures, the equilibrium favors NO2. The fact that equilibrium constants are temperature dependent explains why you may find different values for the equilibrium constant for the same chemical reaction.
| The Temperature Dependence of the Equilibrium Constant for the Dimerization of NO2 | ||||
| Temperature (oC) | Kp | Kc | ||
| 100 | 0.067 | 2.1 | ||
| 25 | 7.1 | 170 | ||
| 0 | 63 | 1400 | ||
| -78 | 25,000,000 | 400,000,000 | ||