Practice Problem 4

Assume the following initial concentrations: (PCl₅) = 0.100 M and (Cl₂) = 0.020 M. Calculate the equilibrium concentrations of PCl₅, PCl₃, and Cl₂ if the equilibrium constant for the decomposition of PCl₅ is 0.030.

Solution

We start by representing the problem as follows.

Before doing anything else, we need to compare the reaction quotient for the initial conditions with the equilibrium constant for the reaction.

Once again, the reaction quotient (Q_c = 0) is smaller than the equilibrium constant (K_c = 0.030). Some of the PCl₅ present initially therefore has to decompose to PCl₃ and Cl₂ before the reaction can come to equilibrium. Because of the stoichiometry of this reaction, the magnitude of the change in the PCl₅ concentration as the reaction comes to equilibrium is equal to the magnitude of the changes in the concentrations of PCl₃ and Cl₂. The problem can therefore be represented as follows.

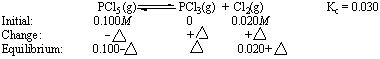
Substituting what we know about the concentrations of PCl₅, PCl₃, and Cl₂ into the equilibrium constant expression for the reaction gives the following result.

Expanding this gives the following quadratic equation.

² + 0.050 - 0.0030 = 0

Solving this equation with the quadratic formula gives the following positive root.

= 0.035 M

This value of can be used to calculate the equilibrium concentrations of the three components of the reaction.

[PCl₅] = 0.100 - = 0.065 M

[PCl₃] = 0 + = 0.035 M

[Cl₂] = 0.020 + = 0.055 M

In this case, only about one-third of the PCl₅ present initially decomposes as the reaction comes to equilibrium.

We can check these results by substituting them into the equilibrium constant expression.

The values for the equilibrium concentrations of PCl₅, PCl₃, and Cl₂ in this calculation must be legitimate because the results of this calculation agree with the equilibrium constant for the reaction, within experimental error.