Practice Problem 5
Ammonia is made from nitrogen and hydrogen by the following reversible reaction.
N2(g) + 3 H2(g)![]() 2 NH3(g)
2 NH3(g)
Assume that the initial concentration of N2 is 0.050 moles per liter and the initial concentration of H2 is 0.100 moles per liter. Calculate the equilibrium concentrations of the three components of this reaction at 500oC if the equilibrium constant for the reaction at this temperature is 0.040.
Solution
We start, as always, by building a representation for the problem based on the following general format.
![]()
We then calculate the initial reaction quotient and compare it with the equilibrium constant for the reaction.
![]()
The reaction quotient (Qc = 0) is smaller than the equilibrium constant (Kc = 0.040), so the reaction has to shift to the right to reach equilibrium. This will result in a decrease in the concentrations of N2 and H2 and an increase in the NH3 concentration. The relationship between the changes in the concentrations of N2, H2, and NH3 as this reaction comes to equilibrium is determined by the stoichiometry of the reaction, as shown in Figure 16.7.
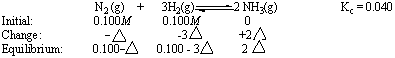
Substituting this information into the equilibrium constant expression for the reaction gives the following equation.
![]()
Since Qc for the initial concentrations and Kc for the reaction are both smaller than 1, let's try the assumption that is small enough that subtracting it from 0.100 -- or even subtracting 3 from 0.100 -- doesn't make a significant change. This assumption gives the following approximate equation.
![]()
Solving this equation for gives the following result.
![]() ~ 1.0 x 10-3
M
~ 1.0 x 10-3
M
Now we have to check our assumptions. Is significantly smaller than 0.100? Yes, is about 1% of the initial concentration of N2.
| 0.001 | x 100% = 1% |
| 0.100 |
Is 3 significantly smaller than 0.100? Once again, the answer is yes, 3 is only about 2% of the initial concentration of H2.
| 3(0.001) | x 100% = 3% |
| 0.100 |
We can therefore use this approximate value of to determine the equilibrium concen- trations of N2, H2, and NH3.
[NH3] = 2![]() ~ 0.0020 M
~ 0.0020 M
[N2] = 0.100- ![]() ~ 0.099 M
~ 0.099 M
[H2] = 0.100 - 3![]() ~0.097
M
~0.097
M
Note that only 1% of the nitrogen is converted into ammonia under these conditions.
We can check the validity of our calculation by substituting this information back into the equilibrium constant expression.
![]()
Once again, we have reason to accept the assumption that is small compared with the initial concentrations because the equilibrium constant calculated from these data agrees with the value of Kc given in the problem within experimental error.