Practice Problem 3

Use half-reactions to balance the equation for the reaction between sulfur dioxide and the dichromate ion in acidic solution.

Solution

STEP 1:Write a skeleton equation for the reaction.

SO₂ + Cr₂O₇^2- SO₄^2- + Cr³⁺

STEP 2: Assign oxidation numbers to atoms on both sides of the equation.

SO2		+ Cr2O72-		SO42-			+ Cr3+
+4	-2	+6 -2		+6	-2		+3

STEP 3: Determine which atoms are oxidized and which are reduced.  

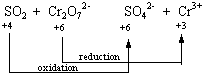
STEP 4: Divide the reaction into oxidation and reduction half-reactions and balance these half-reactions. This reaction can be divided into the following half-reactions.  

Oxidation:			SO2		SO42-
			+4		+6

Reduction:			Cr2O72-		Cr3+
			+6		+3

It doesn't matter which half-reaction we balance first, so let's start with reduction. Because the Cr₂O₇^2- ion contains two chromium atoms that must be reduced from the +6 to the +3 oxidation state, six electrons are consumed in this half-reaction.  

Reduction:

Cr2O72- + 6 e-

2 Cr3+

This raises an interesting question: What happens to the oxygen atoms when the chromium atoms are reduced? The seven oxygen atoms in the Cr₂O₇^2- ions are formally in the -2 oxidation state. If these atoms were released into solution in the -2 oxidation state when the chromium was reduced, they would be present as O^2- ions. But it doesn't make sense to write this half-reaction as follows.  

Reduction:

Cr2O72- + 6 e-

2 Cr3+ + 7 O2-

The reaction is being run in an acidic solution and the O^2- ion is a very strong base that would immediately react with the H⁺ ions in this solution to form water, as shown in the figure below.

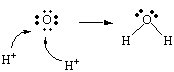
The following is therefore a more realistic equation for this half-reaction.  

Reduction:

Cr2O72- + 14 H+ + 6 e-

2 Cr3+ + 7 H2O

We can now turn to the oxidation half-reaction, and start by noting that two electrons are given off when sulfur is oxidized from the +4 to the +6 oxidation state.  

Oxidation:

SO2

SO42- + 2 e-

The key to balancing the charge on both sides of this equation is remembering that the reaction is run in acid, which contains H⁺ ions and H₂O molecules. We can therefore add H⁺ ions or H₂O molecules to either side of the equation, as needed. The only way to balance the charge on both sides of this equation is to add four H⁺ ions to the products of the reaction.  

Oxidation:

SO2

SO42- + 2 e- + 4 H+

We can then balance the number of hydrogen and oxygen atoms on both sides of this equation by adding a pair of H₂O molecules to the reactants.  

Oxidation:

SO2 + 2 H2O

SO42- + 2 e- + 4 H+

This equation can be understood in terms of the Lewis structures shown in the figure below.

Let's focus, for the moment, on the middle Lewis structure and remove two electrons from the sulfur atom.

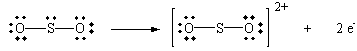
Let's now form two new sulfur-oxygen bonds by donating pairs of non bonding electrons from neighboring water molecules.

The product of this hypothetical reaction can now lose a pair of H⁺ ions to form sulfurinc acid.

STEP 5: Combine the two half-reactions so that electrons are neither created nor destroyed. Six electrons are consumed in the reduction half-reaction and two electrons are given off in the oxidation half-reaction. We can combine these half-reactions so that electrons are conserved by multiplying the reduction half-reaction by 3.

(Cr2O72- + 14 H+ + 6 e- 2 Cr3+ + 7 H2O)

+ 3(SO2 + 2 H2O SO42- + 2 e- + 4 H+)

__________________________________________

Cr2O72- + 3 SO2 + 14 H+ + 6 H2O 2 Cr3+ + 3 SO42- + 12 H+ + 7 H2O

STEP 6: Balance the remainder of the equation by inspection, if necessary. Although the equation appears balanced, we are not quite finished with it. We can simplify the equation by subtracting 12 H⁺ ions and 6 H₂O molecules from each side to generate the following balanced equation.

Cr₂O₇^2-(aq) + 3 SO₂(aq) + 2 H⁺(aq) 2 Cr³⁺(aq) + 3 SO₄^2-(aq) + H₂O(l)