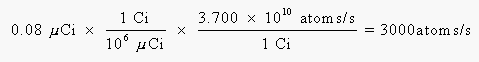
Practice Problem 10

Calculate the rems of radiation absorbed by the average person from the ¹⁴C in his or her body.  Assume the activity of the ¹⁴C in the average body is 0.08 mCi, the energy of the b-particles emitted when ¹⁴C decays is 0.156 MeV, and about one-third of this energy is captured by the body.

Solution

We can calculate the number of b-particles emitted per second from the activity of the ¹⁴C isotope:

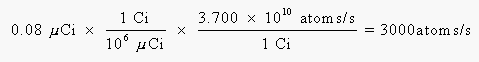
To calculate the effect of this radiation over a year, we have to calculate the number of ¹⁴C nuclei that decay during this time:

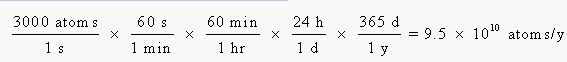
We can now calculate the amount of energy absorbed per year from the number of atoms that disintegrate, the energy per disintegration, and the fraction of this energy absorbed by the body:

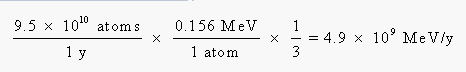
Before we can go any further, we have to convert this energy from units of million electron volts per year to joules per year:

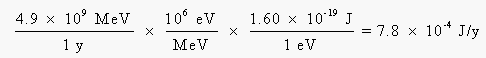
Averaged over a 70-kg body weight, this amounts to about 1 x 10^-5 J per kilogram of body weight per year.  If 1 rad is equal to 0.01 J/kg, the radiation absorbed dose from ¹⁴C decay is 0.001 rad per year.  Using an RBE for b decay of 1, this corresponds to 0.001 rems, or 1 millirem per year.