| The Simplest Repeating Unit in a Crystal | A Three-Dimensional Graph |
| NaCl and ZnS | Measuring the Distance Between Particles |
| Determining the Unit Cell of a Crystal | Calculating Metallic or Ionic Radii |
Unit Cells: The Simplest Repeating Unit in a Crystal
The structure of solids can be described as if they were three-dimensional analogs of a piece of wallpaper. Wallpaper has a regular repeating design that extends from one edge to the other. Crystals have a similar repeating design, but in this case the design extends in three dimensions from one edge of the solid to the other.
We can unambiguously describe a piece of wallpaper by specifying the size, shape, and contents of the simplest repeating unit in the design. We can describe a three-dimensional crystal by specifying the size, shape, and contents of the simplest repeating unit and the way these repeating units stack to form the crystal.
The simplest repeating unit in a crystal is called a unit
cell. Each unit cell is defined in terms of lattice points![]() the
points in space about which the particles are free to vibrate in
a crystal.
the
points in space about which the particles are free to vibrate in
a crystal.
The structures of the unit cell for a variety of salts are shown below.
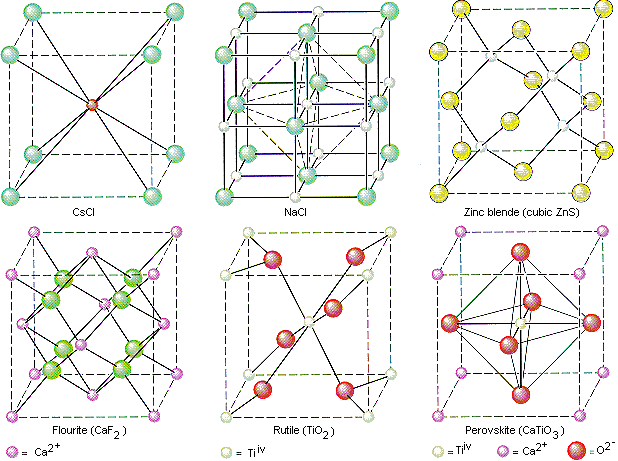
In 1850, Auguste Bravais showed that crystals could be divided into 14 unit cells, which meet the following criteria.
- The unit cell is the simplest repeating unit in the crystal.
- Opposite faces of a unit cell are parallel.
- The edge of the unit cell connects equivalent points.
The 14 Bravais unit cells are shown in the figure below.
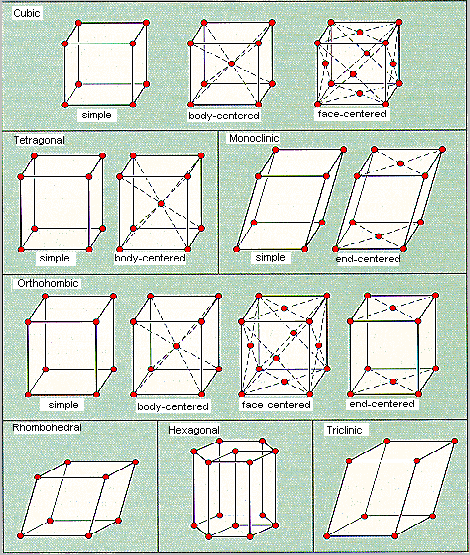
These unit cells fall into seven categories, which differ in the three unit-cell edge lengths (a, b, and c) and three internal angles (a, � and g), as shown in the table below.
The Seven Categories of Bravais Unit Cells
| Category | Edge Lengths | Internal Angles | ||
| Cubic | (a = b = c) | (a = �/i> = g = 90o) | ||
| Tetragonal | (a = b |
(a = �/i> = g = 90o) | ||
| Monoclinic | (a |
(a = �/i> = 90o |
||
| Orthorhombic | (a |
(a = �/i> = g = 90o) | ||
| Rhombohedral | (a = b = c) | (a = �/i> = g |
||
| Hexagonal | (a = b |
(a = �/i> = 90o, g = 120o) | ||
| Triclinic | (a |
(a |
We will focus on the cubic category, which includes the three
types of unit cells![]() simple
cubic, body-centered cubic, and face-centered cubic
simple
cubic, body-centered cubic, and face-centered cubic![]() shown
in the figure below.
shown
in the figure below.

These unit cells are important for two reasons. First, a number of metals, ionic solids, and intermetallic compounds crystallize in cubic unit cells. Second, it is relatively easy to do calculations with these unit cells because the cell-edge lengths are all the same and the cell angles are all 90.
The simple cubic unit cell is the simplest repeating unit in a simple cubic structure. Each corner of the unit cell is defined by a lattice point at which an atom, ion, or molecule can be found in the crystal. By convention, the edge of a unit cell always connects equivalent points. Each of the eight corners of the unit cell therefore must contain an identical particle. Other particles can be present on the edges or faces of the unit cell, or within the body of the unit cell. But the minimum that must be present for the unit cell to be classified as simple cubic is eight equivalent particles on the eight corners.
The body-centered cubic unit cell is the simplest repeating unit in a body-centered cubic structure. Once again, there are eight identical particles on the eight corners of the unit cell. However, this time there is a ninth identical particle in the center of the body of the unit cell.
The face-centered cubic unit cell also starts with identical particles on the eight corners of the cube. But this structure also contains the same particles in the centers of the six faces of the unit cell, for a total of 14 identical lattice points.
The face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure. In fact, the presence of face-centered cubic unit cells in this structure explains why the structure is known as cubic closest-packed.
Unit Cells: A Three-Dimensional Graph
The lattice points in a cubic unit cell can be described in terms of a three-dimensional graph. Because all three cell-edge lengths are the same in a cubic unit cell, it doesn't matter what orientation is used for the a, b, and c axes. For the sake of argument, we'll define the a axis as the vertical axis of our coordinate system, as shown in the figure below.
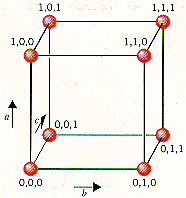
The b axis will then describe movement across the front of the unit cell, and the c axis will represent movement toward the back of the unit cell. Furthermore, we'll arbitrarily define the bottom left corner of the unit cell as the origin (0,0,0). The coordinates 1,0,0 indicate a lattice point that is one cell-edge length away from the origin along the a axis. Similarly, 0,1,0 and 0,0,1 represent lattice points that are displaced by one cell-edge length from the origin along the b and c axes, respectively.
Thinking about the unit cell as a three-dimensional graph allows us to describe the structure of a crystal with a remarkably small amount of information. We can specify the structure of cesium chloride, for example, with only four pieces of information.
- CsCl crystallizes in a cubic unit cell.
- The length of the unit cell edge is 0.4123 nm.
- There is a Cl- ion at the coordinates 0,0,0.
- There is a Cs+ ion at the coordinates 1/2,1/2,1/2.
Because the cell edge must connect equivalent lattice points, the presence of a Cl- ion at one corner of the unit cell (0,0,0) implies the presence of a Cl- ion at every corner of the cell. The coordinates 1/2,1/2,1/2 describe a lattice point at the center of the cell. Because there is no other point in the unit cell that is one cell-edge length away from these coordinates, this is the only Cs+ ion in the cell. CsCl is therefore a simple cubic unit cell of Cl- ions with a Cs+ in the center of the body of the cell.
NaCl should crystallize in a cubic closest-packed array of Cl- ions with Na+ ions in the octahedral holes between planes of Cl- ions. We can translate this information into a unit-cell model for NaCl by remembering that the face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure.
There are four unique positions in a face-centered cubic unit cell. These positions are defined by the coordinates: 0,0,0; 0,1/2,1/2; 1/2,0,1/2; and 1/2,1/2,0. The presence of an particle at one corner of the unit cell (0,0,0) requires the presence of an equivalent particle on each of the eight corners of the unit cell. Because the unit-cell edge connects equivalent points, the presence of a particle in the center of the bottom face (0,1/2,1/2) implies the presence of an equivalent particle in the center of the top face (1,1/2,1/2). Similarly, the presence of particles in the center of the 1/2,0,1/2 and 1/2,1/2,0 faces of the unit cell implies equivalent particles in the centers of the 1/2,1,1/2 and 1/2,1/2,1 faces.
The figure below shows that there is an octahedral hole in the center of a face-centered cubic unit cell, at the coordinates 1/2,1/2,1/2. Any particle at this point touches the particles in the centers of the six faces of the unit cell.
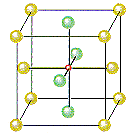
The other octahedral holes in a face-centered cubic unit cell are on the edges of the cell, as shown in the figure below.
If Cl- ions occupy the lattice points of a face-centered cubic unit cell and all of the octahedral holes are filled with Na+ ions, we get the unit cell shown in the figure below.
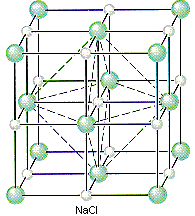
We can therefore describe the structure of NaCl in terms of the following information.
- NaCl crystallizes in a cubic unit cell.
- The cell-edge length is 0.5641 nm.
- There are Cl- ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Na+ ions at the positions 1/2,1/2,1/2; 1/2,0,0; 0,1/2,0; and 0,0,1/2.
Placing a Cl- ion at these four positions implies the presence of a Cl- ion on each of the 14 lattice points that define a face-centered cubic unit. Placing a Na+ ion in the center of the unit cell (1/2,1/2,1/2) and on the three unique edges of the unit cell (1/2,0,0; 0,1/2,0; and 0,0,1/2) requires an equivalent Na+ ion in every octahedral hole in the unit cell.
ZnS crystallizes as cubic closest-packed array of S2- ions with Zn2+ ions in tetrahedral holes. The S2- ions in this crystal occupy the same positions as the Cl- ions in NaCl. The only difference between these crystals is the location of the positive ions. The figure below shows that the tetrahedral holes in a face-centered cubic unit cell are in the corners of the unit cell, at coordinates such as 1/4,1/4,1/4. An atom with these coordinates would touch the atom at this corner as well as the atoms in the centers of the three faces that form this corner. Although it is difficult to see without a three-dimensional model, the four atoms that surround this hole are arranged toward the corners of a tetrahedron.
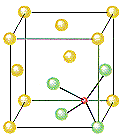
Because the corners of a cubic unit cell are identical, there must be a tetrahedral hole in each of the eight corners of the face-centered cubic unit cell. If S2- ions occupy the lattice points of a face-centered cubic unit cell and Zn2+ ions are packed into every other tetrahedral hole, we get the unit cell of ZnS shown in the figure below.
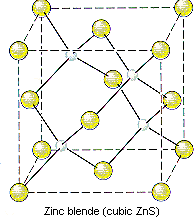
The structure of ZnS can therefore be described as follows.
- ZnS crystallizes in a cubic unit cell.
- The cell-edge length is 0.5411 nm.
- There are S2- ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Zn2+ ions at the positions 1/4,1/4,1/4; 1/4,3/4,3/4; 3/4,1/4,3/4; and 3/4,3/4,1/4.
Note that only half of the tetrahedral holes are occupied in this crystal because there are two tetrahedral holes for every S2- ion in a closest-packed array of these ions.
Unit Cells: Measuring the Distance Between Particles
Nickel is one of the metals that crystallize in a cubic closest-packed structure. When you consider that a nickel atom has a mass of only 9.75 x 10-23 g and an ionic radius of only 1.24 x 10-10 m, it is a remarkable achievement to be able to describe the structure of this metal. The obvious question is: How do we know that nickel packs in a cubic closest-packed structure?
The only way to determine the structure of matter on an atomic scale is to use a probe that is even smaller. One of the most useful probes for studying matter on this scale is electromagnetic radiation.
In 1912, Max van Laue found that x-rays that struck the surface of a crystal were diffracted into patterns that resembled the patterns produced when light passes through a very narrow slit. Shortly thereafter, William Lawrence Bragg, who was just completing his undergraduate degree in physics at Cambridge, explained van Laue's resultswith an equation known as the Bragg equation, which allows us to calculate the distance between planes of atoms in a crystal from the pattern of diffraction of x-rays of known wavelength.
n![]() = 2d sin T
= 2d sin T
The pattern by which x-rays are diffracted by nickel metal suggests that this metal packs in a cubic unit cell with a distance between planes of atoms of 0.3524 nm. Thus, the cell-edge length in this crystal must be 0.3524 nm. Knowing that nickel crystallizes in a cubic unit cell is not enough. We still have to decide whether it is a simple cubic, body-centered cubic, or face-centered cubic unit cell. This can be done by measuring the density of the metal.
Unit Cells: Determining the Unit Cell of a Crystal
Atoms on the corners, edges, and faces of a unit cell are shared by more than one unit cell, as shown in the figure below. An atom on a face is shared by two unit cells, so only half of the atom belongs to each of these cells. An atom on an edge is shared by four unit cells, and an atom on a corner is shared by eight unit cells. Thus, only one-quarter of an atom on an edge and one-eighth of an atom on a corner can be assigned to each of the unit cells that share these atoms.

If nickel crystallized in a simple cubic unit cell, there would be a nickel atom on each of the eight corners of the cell. Because only one-eighth of these atoms can be assigned to a given unit cell, each unit cell in a simple cubic structure would have one net nickel atom.
Simple cubic structure:
8 corners x 1/8 = 1 atom
If nickel formed a body-centered cubic structure, there would be two atoms per unit cell, because the nickel atom in the center of the body wouldn't be shared with any other unit cells.
Body-centered cubic structure:
(8 corners x 1/8) + 1 body = 2 atoms
If nickel crystallized in a face-centered cubic structure, the six atoms on the faces of the unit cell would contribute three net nickel atoms, for a total of four atoms per unit cell.
Face-centered cubic structure:
(8 corners x 1/8) + (6 faces x 1/2) = 4 atoms
Because they have different numbers of atoms in a unit cell, each of these structures would have a different density. Let's therefore calculate the density for nickel based on each of these structures and the unit cell edge length for nickel given in the previous section: 0.3524 nm. In order to do this, we need to know the volume of the unit cell in cubic centimeters and the mass of a single nickel atom.
The volume (V) of the unit cell is equal to the cell-edge length (a) cubed.
V = a3 = (0.3524 nm)3 = 0.04376 nm3
Since there are 109 nm in a meter and 100 cm in a meter, there must be 107 nm in a cm.

We can therefore convert the volume of the unit cell to cm3 as follows.

The mass of a nickel atom can be calculated from the atomic weight of this metal and Avogadro's number.

The density of nickel, if it crystallized in a simple cubic structure, would therefore be 2.23 g/cm3, to three significant figures.
Simple cubic structure:

Because there would be twice as many atoms per unit cell if nickel crystallized in a body-centered cubic structure, the density of nickel in this structure would be twice as large.
Body-centered cubic structure:

There would be four atoms per unit cell in a face-centered cubic structure and the density of nickel in this structure would be four times as large.
Face-centered cubic structure:
The experimental value for the density of nickel is 8.90 g/cm3. The obvious conclusion is that nickel crystallizes in a face-centered cubic unit cell and therefore has a cubic closest-packed structure.
Unit Cells: Calculating Metallic or Ionic Radii
Estimates of the radii of most metal atoms can be found. Where do these data come from? How do we know, for example, that the radius of a nickel atom is 0.1246 nm?
Nickel crystallizes in a face-centered cubic unit cell with a cell-edge length of 0.3524 nm to calculate the radius of a nickel atom.
One of the faces of a face-centered cubic unit cell is shown in the figure below.

According to this figure, the diagonal across the face of this unit cell is equal to four times the radius of a nickel atom.
![]()
The Pythagorean theorem states that the diagonal across a right triangle is equal to the sum of the squares of the other sides. The diagonal across the face of the unit cell is therefore related to the unit-cell edge length by the following equation.
![]()
Taking the square root of both sides gives the following result.
![]()
We now substitute into this equation the relationship between the diagonal across the face of this unit cell and the radius of a nickel atom:
![]()
Solving for the radius of a nickel atom gives a value of 0.1246 nm:

A similar approach can be taken to estimating the size of an ion. Let's start by using the fact that the cell-edge length in cesium chloride is 0.4123 nm to calculate the distance between the centers of the Cs+ and Cl- ions in CsCl.
CsCl crystallizes in a simple cubic unit cell of Cl- ions with a Cs+ ion in the center of the body of the cell, as shown in the figure below.

Before we can calculate the distance between the centers of the Cs+ and Cl- ions in this crystal, however, we have to recognize the validity of one of the simplest assumptions about ionic solids: The positive and negative ions that form these crystals touch.
We can therefore assume that the diagonal across the body of the CsCl unit cell is equivalent to the sum of the radii of two Cl- ions and two Cs+ ions.
![]()
The three-dimensional equivalent of the Pythagorean theorem suggests that the square of the diagonal across the body of a cube is the sum of the squares of the three sides.
![]()
Taking the square root of both sides of this equation gives the following result.
![]()
If the cell-edge length in CsCl is 0.4123 nm, the diagonal across the body in this unit cell is 0.7141 nm.
![]()
The sum of the ionic radii of Cs+ and Cl- ions is half this distance, or 0.3571 nm.

If we had an estimate of the size of either the Cs+ or Cl- ion, we could use the results to calculate the radius of the other ion. The ionic radius of the Cl- ion is 0.181 nm. Substituting this value into the last equation gives a value of 0.176 nm for the radius of the Cs+ ion.
![]()
![]()
![]()
The results of this calculation are in reasonable agreement with the value of 0.169 nm known for the radius of the Cs+ ion. The discrepancy between these values reflects the fact that ionic radii vary from one crystal to another. The tabulated values are averages of the results of a number of calculations of this type.

