Solving Equilibrium Problems Involving Weak Acids
Example: Consider the process by which we would calculate the H 3O+, OAc-, and HOAc concentrations at equilibrium in an 0.10 M solution of acetic acid in water.
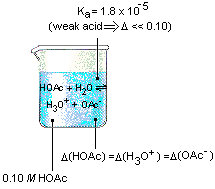
We start this calculation by building a representation of what we know about the reaction.
| HOAc(aq) | + | H2O(l) | H3O+(aq) | + | OAc-(aq) | Ka = 1.8 x 10-5 | |||
| Initial: | 0.10 M | 0 | 0 | ||||||
| Equilibrium: | ? | ? | ? |
We then compare the initial reaction quotient (Qa) with the equilibrium constant (Ka) for the reaction and reach the obvious conclusion that the reaction must shift to the right to reach equilibrium.

Recognizing that we get one H3O+ ion and one OAc- ion each time an HOAc molecule dissociates allows us to write equations for the equilibrium concentrations of the three components of the reaction.
| HOAc(aq) | + | H2O(l) | H3O+(aq) | + | OAc-(aq) | Ka = 1.8 x 10-5 | |||
| Initial: | 0.10 M | 0 | 0 | ||||||
| Equilibrium: | 0.10 - |
Substituting what we know about the system at equilibrium into the Ka expression gives the following equation.

Although we could rearrange this equation and solve it with
the quadratic formula, it is tempting to test the assumption that
![]() C
is small compared with the initial concentration of acetic acid.
C
is small compared with the initial concentration of acetic acid.

We then solve this approximate equation for the value of ![]() C.
C.
![]() C
C ![]() 0.0013
0.0013
![]() C is small enough to be ignored in this
problem because it is less than 5% of the initial concentration
of acetic acid.
C is small enough to be ignored in this
problem because it is less than 5% of the initial concentration
of acetic acid.

We can therefore use this value of ![]() C
to calculate the equilibrium concentrations of H3O+,
OAc-, and HOAc.
C
to calculate the equilibrium concentrations of H3O+,
OAc-, and HOAc.
[HOAc] = 0.10 - ![]() C
C ![]() 0.10 M
0.10 M
[H3O+] = [OAc-]
= ![]() C
C ![]() 0.0013 M
0.0013 M
We can confirm the validity of these results by substituting these concentrations into the expression for Ka.

Our calculation must be valid because the ratio of these concentrations agrees with the value of Ka for acetic acid, within experimental error.
Hidden Assumptions In Weak-Acid Calculations
When solving problems involving weak acids, it may appear that
one assumption is made![]() that
that
![]() is small compared with the initial concentration of HOAc. In
fact, two assumptions are made.
is small compared with the initial concentration of HOAc. In
fact, two assumptions are made.
The second assumption is hidden in the way the problem is set up.
| HOAc(aq) | + | H2O(l) | H3O+(aq) | + | OAc-(aq) | Ka = 1.8 x 10-5 | |||
| Initial: | 0.10 M | 0 | 0 | ||||||
| Equilibrium: | 0.10 - |
The amount of H3O+ ion in water is so small that we are tempted to assume that the initial concentration of this ion is zero, which isn't quite true.
It is important to remember that there are two sources of the H3O+ ion in this solution. We get H3O+ ions from the dissociation of acetic acid.
HOAc(aq) + H2O(l)
![]() H3O+(aq) + OAc-(aq)
H3O+(aq) + OAc-(aq)
But we also get H3O+ ions from the dissociation of water.
2 H2O(l) ![]() H3O+(aq) + OH-(aq)
H3O+(aq) + OH-(aq)

Because the initial concentration of the H3O+
ion is not quite zero, it might be a better idea to write "![]() 0" beneath
the H3O+ term when we describe the initial
conditions of the reaction, as shown below.
0" beneath
the H3O+ term when we describe the initial
conditions of the reaction, as shown below.
| HOAc(aq) | + | H2O(l) | H3O+(aq) | + | OAc-(aq) | Ka = 1.8 x 10-5 | |||||
| Initial: | 1.0 M | 0 | |||||||||
| Equilibrium: | 1.0 - |
Before we can trust the results of the calculation for acetic acid in the previous section, we have to check both of the assumptions made in this calculation.
- The assumption that the amount of acid that dissociates is small compared with the initial concentration of the acid.
- The assumption that enough acid dissociates to allow us to ignore the dissociation of water
We have already confirmed the validity of the first assumption. (Only 1.3% of the acetic acid molecules dissociate in this solution.) Let's now check the second assumption.
According to the calculation in the previous section, the concentration of the H3O+ ion from the dissociation of acetic acid is 0.0013 M. The OH- ion concentration in this solution is therefore 7.7 x 10-12 M.
All of the OH- ion in this solution comes from the dissociation of water. Since we get one H3O+ ion for each OH- ion when water dissociates, the contribution to the total H3O+ ion concentration from the dissociation of water must be 7.7 x 10-12 M. In other words, only about 6 parts per billion of the H3O+ ions in this solution come from the dissociation of water.
![]()
The second assumption is therefore valid in this calculation. For all practical purposes, we can assume that virtually none of the H3O+ ion in this solution comes from the dissociation of water. As might be expected, this assumption only fails for dilute solutions of very weak acids.
Implications of the Assumptions In Weak-Acid Calculations
The two assumptions that are made in weak-acid equilibrium problems can be restated as follows.
- The dissociation of the acid is small enough that the change in the concentration of the acid as the reaction comes to equilibrium can be ignored.
- The dissociation of the acid is large enough that the H3O+ ion concentration from the dissociation of water can be ignored.
In other words, the acid must be weak enough that ![]() C
is small compared with the initial concentration of the acid. But
it also must be strong enough that the H3O+
ions from the acid overwhelm the dissociation of water. In order
for the approach taken to the calculation for acetic acid to
work, the acid has to be "just right." If it's too
strong,
C
is small compared with the initial concentration of the acid. But
it also must be strong enough that the H3O+
ions from the acid overwhelm the dissociation of water. In order
for the approach taken to the calculation for acetic acid to
work, the acid has to be "just right." If it's too
strong, ![]() C won't be small enough to be ignored. If
it's too weak, the dissociation of water will have to be included
in the calculation.
C won't be small enough to be ignored. If
it's too weak, the dissociation of water will have to be included
in the calculation.
Fortunately, many acids are "just right." To illustrate this point, the next section will use both assumptions in a series of calculations designed to identify the factors that influence the H3O+ ion concentration in aqueous solutions of weak acids.
Factors that Influence the H3O+ Ion Concentration in Weak-Acid Solutions

The following examples probe the relationship between the H3O+ ion concentration at equilibrium and the acid-dissociation equilibrium constant for the acid.
| Practice Problem 1: Calculate the pH of 0.10 M solution of hypochlorous acid, HOCl, Ka = 2.9 x 10-8 |
As expected, the H3O+
ion concentration at equilibrium ![]() and
therefore the pH of the solution
and
therefore the pH of the solution![]() depends
on the value of Ka for the acid. The
H3O+
ion concentration decreases and the pH of the solution increases
as the value of Ka
becomes smaller. The next exercise shows that the H3O+
ion concentration at equilibrium also depends on the initial
concentration of the acid.
depends
on the value of Ka for the acid. The
H3O+
ion concentration decreases and the pH of the solution increases
as the value of Ka
becomes smaller. The next exercise shows that the H3O+
ion concentration at equilibrium also depends on the initial
concentration of the acid.
| Practice Problem 2: Calculate the H3O+ ion concentration and the pH of acetic acid solutions with the following concentrations: 1.0 M, 0.10 M, and 0.01 M. |
The concentration of the H3O+ ion in an aqueous solution gradually decreases and the pH of the solution increases as the solution becomes more dilute.
The results of the previous two examples provide a basis for constructing a model that allows us to predict when we can ignore the dissociation of water in equilibrium problems involving weak acids. Two factors must be built into this model: (1) the strength of the acid as reflected by the value of Ka, and (2) the strength of the solution as reflected by the initial concentration of the acid.
Solving Equilibrium Problems Involving Not-So-Weak Acids
We need to develop techniques to handle problems for which one
or the other of our assumptions is not
valid. (Either the acid is not weak enough to ignore the value of
![]() C,
or the acid is so weak we have to include the dissociation of
water in our calculations.)
C,
or the acid is so weak we have to include the dissociation of
water in our calculations.)
In this section, we will consider acid solutions that aren't
weak enough to ignore the value of ![]() C. Let's start by
calculating the H3O+, HClO2, and
ClO2- concentrations at equilibrium in an
0.10 M solution of chlorous acid (Ka
= 1.1 x 10-2).
C. Let's start by
calculating the H3O+, HClO2, and
ClO2- concentrations at equilibrium in an
0.10 M solution of chlorous acid (Ka
= 1.1 x 10-2).

HClO2(aq) + H2O(l)
![]() H3O+(aq) + ClO2-(aq)
H3O+(aq) + ClO2-(aq)
The first step, as always, involves building a representation of the problem.
| HClO2(aq) | + | H2O(l) | H3O+(aq) | + | ClO2-(aq) | Ka = 1.1 x 10-2 | |||
| Initial: | 0.10 M | 0 | |||||||
| Equilibrium: | 0.10 - |
We then substitute this information into the Ka expression.

The value of Ka for this acid is
close enough to 1 to make us suspicious of the assumption that ![]() C
is small compared with the initial concentration of the acid.
There is nothing wrong with trying this assumption, however, even
if we suspect it isn't valid.
C
is small compared with the initial concentration of the acid.
There is nothing wrong with trying this assumption, however, even
if we suspect it isn't valid.

Solving this approximate equation gives a value for ![]() C
that is 33% of the initial concentration of chlorous acid.
C
that is 33% of the initial concentration of chlorous acid.
![]() C
C ![]() 0.033 M
0.033 M
The assumption that ![]() C is small therefore fails
miserably.
C is small therefore fails
miserably.
There are two ways out of this difficulty. We can expand the
original equation and solve it by the quadratic formula. Or we
can use successive approximations to solve the problem. Both
techniques give the following value of ![]() C
for this problem.
C
for this problem.
![]() C = 0.028
C = 0.028
Using this value of ![]() C gives the following results.
C gives the following results.
| [HClO2] | = 0.10 - |
= 0.072 M |
| [H3O+] | = [ClO2-] | = |
Chlorous acid doesn't belong among the class of strong acids that dissociate more or less completely. Nor does it fit in the category of weak acids, which dissociate only to a negligible extent. Since the amount of dissociation in this solution is about 28%, it might be classified as a "not-so-weak acid."
Solving Equilibrium Problems Involving Very Weak Acids
It is more difficult to solve equilibrium problems when the acid is too weak to ignore the dissociation of water. Deriving an equation that can be used to solve this class of problems is therefore easier than solving them one at a time. To derive such an equation, we start by assuming that we have a generic acid, HA, that dissolves in water. We therefore have two sources of the H3O+ ion.
HA(aq) + H2O(l)
![]() H3O+(aq)
+ A-(aq)
H3O+(aq)
+ A-(aq)
2 H2O(l) ![]() H3O+(aq) + OH-(aq)
H3O+(aq) + OH-(aq)
Because we get one H3O+ ion for each OH- ion when water dissociates, the concentration of the H3O+ ion from the dissociation of water is always equal to the amount of OH- ion from this reaction.
[H3O+]W = [OH-]W
The total H3O+ ion concentration in an acid solution is equal to the sum of the H3O+ ion concentrations from the two sources of this ion, the acid and water.
[H3O+]T = [H3O+]HA + [H3O+]W
We now write three more equations that describe this system. The first equation is the equilibrium constant expression for this reaction.

The second equation summarizes the relationship between the total H3O+ ion concentration in the solution and the OH- ion concentration from the dissociation of water.
[H3O+]T [OH-]W = Kw
The third equation summarizes the relationship between the positive and negative ions produced by the two reactions that occur in this solution.
[H3O+]T = [A-] + [OH-]W
(This equation simply states that the sum of the positive ions formed by the dissociation of the acid and water is equal to the sum of the negative ions produced by these reactions.)
We now substitute the second equation into the third.

We then solve this equation for the [A-] term.

We then substitute this equation into the equilibrium constant expression.
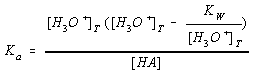
Rearranging this equation by combining terms gives the following result.
Ka[HA] = [H3O+]T2 - Kw
We then solve this equation for the H3O+ ion concentration and take the square root of both sides.
![]()
We can generate a more useful version of this equation by
remembering that we are trying to solve equilibrium problems for
acids that are so weak we can't ignore the dissociation of water.
We can therefore assume that ![]() C is small compared
with the initial concentration of the acid.
C is small compared
with the initial concentration of the acid.
By convention, the symbol used to represent the initial
concentration of the acid is Ca. If ![]() C
is small compared with the initial concentration of the acid,
then the concentration of HA when this reaction reaches
equilibrium will be virtually the same as the initial
concentration.
C
is small compared with the initial concentration of the acid,
then the concentration of HA when this reaction reaches
equilibrium will be virtually the same as the initial
concentration.
[HA] ![]() Ca
Ca
Substituting this approximation into the equation derived in this section gives an equation that can be used to calculate the pH of a solution of a very weak acid.
![]()
| Practice Problem 3: Calculate the H3O+ concentration in an 0.0001 M solution of hydrocyanic acid (HCN). HCN(aq) + H2O(l)
|
Summarizing the Chemistry of Weak Acids
This section compares the way in which the H3O+ concentration is calculated for pure water, a weak acid, and a very weak acid.
The product of the concentrations of the H3O+ and OH- ions in pure water is equal to Kw.
[H3O+][OH-] = Kw
But the H3O+ and OH- ion concentrations in pure water are the same.
[H3O+] = [OH-]
Substituting the second equation into the first gives the following result.
[H3O+]2 = Kw
The H3O+ ion concentration in pure water is therefore equal to the square root of Kw.
![]()
The generic equilibrium constant expression for a weak acid is written as follows.

If the acid is strong enough to ignore the dissociation of water, the H3O+ ion and A- ion concentrations in this solution are about equal.
[H3O+] ![]() [A-]
[A-]
Substituting this information into the acid-dissociation equilibrium constant expression gives the following result.

The concentration of the HA molecules at equilibrium is equal
to the initial concentration of the acid minus the amount that
dissociates: ![]() C.
C.

If ![]() C is small compared with the initial
concentration of the acid, we get the following approximate
equation.
C is small compared with the initial
concentration of the acid, we get the following approximate
equation.

Rearranging this equation and taking the square root of both sides gives the following result.
![]()
When the acid is so weak that we can't ignore the dissociation of water, we use the following equation to calculate the concentration of the H3O+ ion at equilibrium.
![]()
The equations used to calculate the H3O+ ion concentration in these solutions are summarized below.
| Pure Water: | |||
| Weak Acid: | |||
| Very Weak Acid: |
The first and second equations are nothing more than special
cases of the third. When we can ignore the dissociation of the
acid![]() because
there is no acid in the solution
because
there is no acid in the solution![]() we
get the first equation. When we can ignore the dissociation of
water, we get the second equation. When we can't ignore the
dissociation of either the acid or water, we have to use the last
equation.
we
get the first equation. When we can ignore the dissociation of
water, we get the second equation. When we can't ignore the
dissociation of either the acid or water, we have to use the last
equation.
This discussion gives us a basis for deciding when we can ignore the dissociation of water. Remember our rule of thumb: we can ignore anything that makes a contribution of less than 5% to the total. Now compare the most inclusive equation for the H3O+ ion concentration
![]()
with the equation that assumes that the dissociation of water can be ignored.
![]()
The only difference is the Kw term, which is under the square root sign.
As a rule: We can ignore the dissociation of water when KaCa for a weak acid is larger than 1.0 x 10-13. When KaCa is smaller than 1.0 x 10-13, the dissociation of water must be included in the calculation.
| Practice Problem 4: Calculate the pH of an 0.023 M solution of saccharin (HSc), if Ka is 2.1 x 10-12 for this artificial sweetener. |

