Early studies of radioactivity indicated that
three different kinds of radiation were emitted, symbolized by the first three letters of
the Greek alphabet 
,
�/i>, and 
. With
time, it became apparent that this classification scheme was much too simple. The emission
of a negatively charged �/i>- particle,
for example, is only one example of a family of radioactive transformations known as �/em>-decay. A fourth category, known as spontaneous fission, also had
to be added to describe the process by which certain radioactive nuclides decompose into
fragments of different weight.
Alpha decay is usually restricted to the heavier
elements in the periodic table. (Only a handful of nuclides with atomic numbers less than
83 emit an -particle.)
The product of -decay
is easy to predict if we assume that both mass and charge are conserved in nuclear
reactions. Alpha decay of the 238U "parent" nuclide, for example,
produces 234Th as the "daughter" nuclide.
The sum of the mass numbers of the products (234 + 4) is equal to the mass number of the parent nuclide (238), and the sum of the charges on the products (90 + 2) is equal to the charge on the parent nuclide.
There are three different modes of beta decay:
|
|
|
Electron (�/em>-) emission is literally the process in which an electron is ejected or emitted from the nucleus. When this happens, the charge on the nucleus increases by one. Electron (�/i>-) emitters are found throughout the periodic table, from the lightest elements (3H) to the heaviest (255Es). The product of �/i>--emission can be predicted by assuming that both mass number and charge are conserved in nuclear reactions. If 40K is a �/i>--emitter, for example, the product of this reaction must be 40Ca.
Once again the sum of the mass numbers of the products is equal to the mass number of the parent nuclide and the sum of the charge on the products is equal to the charge on the parent nuclide.
Nuclei can also decay by capturing one of the electrons that surround the nucleus. Electron capture leads to a decrease of one in the charge on the nucleus. The energy given off in this reaction is carried by an x-ray photon, which is represented by the symbol hv, where h is Planck's constant and v is the frequency of the x-ray. The product of this reaction can be predicted, once again, by assuming that mass and charge are conserved.
The electron captured by the nucleus in this reaction is usually a 1s electron because electrons in this orbital are the closest to the nucleus.
A third form of beta decay is called positron (�sup>+) emission. The positron is the antimatter equivalent of an electron. It has the same mass as an electron, but the opposite charge. Positron (�/i>+) decay produces a daughter nuclide with one less positive charge on the nucleus than the parent.
Positrons have a very short life-time. They rapidly lose
their kinetic energy as they pass through matter. As soon as they come to rest, they
combine with an electron to form two -ray photons in a matter-antimatter annihilation reaction.
Thus, although it is theoretically possible to observe a fourth mode of beta decay corresponding to the capture of a positron, this reaction does not occur in nature.
Note that in all three forms of �/i>-decay for the 40K nuclide the mass number of the parent and daughter nuclides are the same for electron emission, electron capture, and position emission. All three forms of �/i>-decay therefore interconvert isobars.
The daughter nuclides produced by -decay or �/i>-decay
are often obtained in an excited state. The excess energy associated with this excited
state is released when the nucleus emits a photon in the -ray portion of the electromagnetic spectrum. Most of
the time, the -ray is
emitted within 10-12 seconds after the -particle or �/i>-particle. In some cases, gamma
decay is delayed, and a short-lived, or metastable, nuclide is formed, which is
identified by a small letter m written after the mass number. 60mCo,
for example, is produced by the electron emission of 60Fe.
The metastable 60mCo nuclide has a
half-life of 10.5 minutes. Since electromagnetic radiation carries neither charge nor
mass, the product of -ray
emission by 60mCo is 60Co.
Nuclides with atomic numbers of 90 or more undergo a form of radioactive decay known as spontaneous fission in which the parent nucleus splits into a pair of smaller nuclei. The reaction is usually accompanied by the ejection of one or more neutrons.
For all but the very heaviest
isotopes, spontaneous fission is a very slow reaction. Spontaneous fission of 238U,
for example, is almost two million times slower than the rate at which this nuclide
undergoes -decay.
| Practice Problem 3: Predict the products of the following nuclear reactions: (a) electron emission by 14C (b) positron emission by 8B (c) electron capture by 125I (d) alpha emission by 210Rn (e) gamma-ray emission by 56mNi |
Neutron-Rich Versus Neutron-Poor Nuclides
In 1934 Enrico Fermi proposed a theory that explained the three forms of beta decay. He argued that a neutron could decay to form a proton by emitting an electron. A proton, on the other hand, could be transformed into a neutron by two pathways. It can capture an electron or it can emit a positron. Electron emission therefore leads to an increase in the atomic number of the nucleus.
Both electron capture and positron emission, on the other hand, result in a decrease in the atomic number of the nucleus.
A plot of the number of neutrons versus the number of protons for all of the stable naturally occurring isotopes is shown in the figure below. Several conclusions can be drawn from this plot.
 |
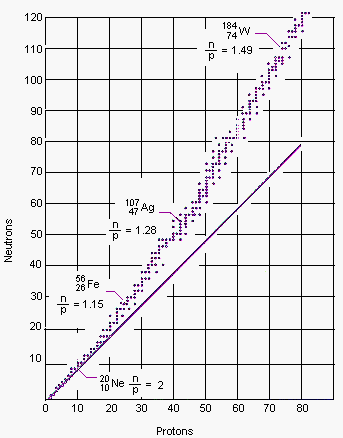| A graph of the number of neutrons versus the number of protons for all stable naturally occurring nuclei. Nuclei that lie to the right of this band of stability are neutron poor; nuclei to the left of the band are neutron-rich. The solid line represents a neutron to proton ratio of 1:1. |
- The stable nuclides lie in a very narrow band of neutron-to-proton ratios.
- The ratio of neutrons to protons in stable nuclides gradually increases as the number of protons in the nucleus increases.
- Light nuclides, such as 12C, contain about the same number of neutrons and protons. Heavy nuclides, such as 238U, contain up to 1.6 times as many neutrons as protons.
- There are no stable nuclides with atomic numbers larger than 83.
- This narrow band of stable nuclei is surrounded by a sea of instability.
- Nuclei that lie above this line have too many neutrons and are therefore neutron-rich.
- Nuclei that lie below this line don't have enough neutrons and are therefore neutron-poor.
The most likely mode of decay for a neutron-rich nucleus is one that converts a neutron into a proton. Every neutron-rich radioactive isotope with an atomic number smaller 83 decays by electron (�/i>-) emission. 14C, 32P, and 35S, for example, are all neutron-rich nuclei that decay by the emission of an electron.
Neutron-poor nuclides decay by modes that convert a proton into a neutron. Neutron-poor nuclides with atomic numbers less than 83 tend to decay by either electron capture or positron emission. Many of these nuclides decay by both routes, but positron emission is more often observed in the lighter nuclides, such as 22Na.
Electron capture is more common among heavier nuclides, such as 125I, because the 1s electrons are held closer to the nucleus of an atom as the charge on the nucleus increases.
A third mode of decay is observed in neutron-poor
nuclides that have atomic numbers larger than 83. Although it is not obvious at first, -decay increases the ratio
of neutrons to protons. Consider what happens during the -decay of 238U,
for example.
The parent nuclide (238U) in this reaction has 92 protons and 146 neutrons, which means that the neutron-to-proton ratio is 1.587. The daughter nuclide (234Th) has 90 protons and 144 neutrons, so its neutron-to-proton ratio is 1.600. The daughter nuclide is therefore slightly less likely to be neutron-poor, as shown in the figure below.
 |
| Practice Problem 4: Predict the most likely modes of decay and the products of decay of the following nuclides: (a) 17F (b) 105Ag (c) 185Ta |
We should be able to predict the mass of an atom from the masses of the subatomic particles it contains. A helium atom, for example, contains two protons, two neutrons, and two electrons.
Example:
The mass of a helium atom should be 4.0329802 amu.
| 2(1.0072765) amu | = | 2.0145530 amu |
| 2(1.0086650) amu | = | 2.0173300 amu |
| 2(0.0005486) amu | = | 0.0010972 amu |
| Total mass | = | 4.0329802 amu |
When the mass of a helium atom is measured, we find that the experimental value is smaller than the predicted mass by 0.0303769 amu.
| Predicted mass | = | 4.0329802 amu |
| Observed mass | = | 4.0026033 amu |
| Mass defect | = | 0.0303769 amu |
The difference between the mass of an atom and the sum of the masses of its protons, neutrons, and electrons is called the mass defect. The mass defect of an atom reflects the stability of the nucleus. It is equal to the energy released when the nucleus is formed from its protons and neutrons. The mass defect is therefore also known as the binding energy of the nucleus.
The binding energy serves the same function for nuclear
reactions as 
H for a chemical reaction. It
measures the difference between the stability of the products of the reaction and the
starting materials. The larger the binding energy, the more stable the nucleus. The
binding energy can also be viewed as the amount of energy it would take to rip the nucleus
apart to form isolated neutrons and protons. It is therefore literally the energy that
binds together the neutrons and protons in the nucleus.
The binding energy of a nuclide can be calculated from its mass defect with Einstein's equation that relates mass and energy.
E = mc2
Example:
We found the mass defect of He to be 0.0303769 amu. To obtain the binding energy in units of joules, we must convert the mass defect from atomic mass units to kilograms.
Multiplying the mass defect in kilograms by the square of the speed of light in units of meters per second gives a binding energy for a single helium atom of 4.53358 x 10-12 joules.
Multiplying the result of this calculation by the number of atoms in a mole gives a binding energy for helium of 2.730 x 1012 joules per mole, or 2.730 billion kilojoules per mole.
This calculation helps us understand the fascination of nuclear reactions. The energy released when natural gas is burned is about 800 kJ/mol. The synthesis of a mole of helium releases 3.4 million times as much energy.
Since most nuclear reactions are carried out on very small samples of material, the mole is not a reasonable basis of measurement. Binding energies are usually expressed in units of electron volts (eV) or million electron volts (MeV) per atom.
Example:
The binding energy of helium is 28.3 x 106 eV/atom or 28.3 MeV/atom.
Calculations of the binding energy can be simplified by using the following conversion factor between the mass defect in atomic mass units and the binding energy in million electron volts.
1 amu = 931.5016 MeV
| Practice Problem 5: Calculate the binding energy of 235U if the mass of this nuclide is 235.0349 amu. |
Binding energies gradually increase with atomic number, although they tend to level off near the end of the periodic table. A more useful quantity is obtained by dividing the binding energy for a nuclide by the total number of protons and neutrons it contains. This quantity is known as the binding energy per nucleon.
The binding energy per nucleon ranges from about 7.5 to 8.8 MeV for most nuclei, as shown in the figure below. It reaches a maximum, however, at an atomic mass of about 60 amu. The largest binding energy per nucleon is observed for 56Fe, which is the most stable nuclide in the periodic table.
 |
The graph of binding energy per nucleon versus atomic mass explains why energy is released when relatively small nuclei combine to form larger nuclei in fusion reactions.
It also explains why energy is released when relatively heavy nuclei split apart in fission (literally, "to split or cleave") reactions.
There are a number of small irregularities in the binding
energy curve at the low end of the mass spectrum, as shown in the figure below. The 4He
nucleus, for example, is much more stable than its nearest neighbors. The unusual
stability of the 4He nucleus explains why -particle decay is usually much faster than the
spontaneous fission of a nuclide into two large fragments.
The Kinetics of Radioactive Decay
Radioactive nuclei decay by first-order kinetics. The rate of radioactive decay is therefore the product of a rate constant (k) times the number of atoms of the isotope in the sample (N).
Rate = kN
The rate of radioactive decay doesn't depend on the chemical state of the isotope. The rate of decay of 238U, for example, is exactly the same in uranium metal and uranium hexafluoride, or any other compound of this element.
The rate at which a radioactive isotope decays is called the activity of the isotope. The most common unit of activity is the curie (Ci), which was originally defined as the number of disintegrations per second in 1 gram of 226Ra. The curie is now defined as the amount of radioactive isotope necessary to achieve an activity of 3.700 x 1010 disintegrations per second.
| Practice Problem 6: The most abundant isotope of uranium is 238U; 99.276% of the atoms in a sample of uranium are 238U. Calculate the activity of the 238U in 1 L of a 1.00 M solution of the uranyl ion, UO22+. Assume that the rate constant for the decay of this isotope is 4.87 x 10-18 disintegrations per second. |
The relative rates at which radioactive nuclei decay can be expressed in terms of either the rate constants for the decay or the half-lives of the nuclei. We can conclude that 14C decays more rapidly than 238U, for example, by noting that the rate constant for the decay of 14C is much larger than that for 238U.
| 14C: | k = 1.210 x 10-4 y-1 | |
| 238U: | k = 1.54 x 10-10 y-1 |
We can reach the same conclusion by noting that the half-life for the decay of 14C is much shorter than that for 235U.
| 14C: | t1/2 = 5730 y | |
| 238U: | t1/2 = 4.51 x 109 y |
The half-life for the decay of a radioactive nuclide is the length of time it takes for exactly half of the nuclei in the sample to decay. In our discussion of the kinetics of chemical reactions, we concluded that the half-life of a first-order process is inversely proportional to the rate constant for this process.
| Practice Problem 7: Calculate the fraction of 14C that remains in a sample after eight half-lives. |
The half-life of a nuclide can be used to estimate the amount of a radioactive isotope left after a given number of half-lives. For more complex calculations, it is easier to convert the half-life of the nuclide into a rate constant and then use the integrated form of the first-order rate law described in the kinetic section.
| Practice Problem 8: How long would it take for a sample of 222Rn that weighs 0.750 g to decay to 0.100 g? Assume a half-life for 222Rn of 3.823 days. |
The earth is constantly bombarded by cosmic rays emitted
by the sun. The total energy received in the form of cosmic rays is small 
no more than the energy received by the
planet from starlight. But the energy of a single cosmic ray is very large, on the order
of several billion electron volts (0.200 million kJ/mol). These highly energetic rays react with atoms
in the atmosphere to produce neutrons that then react with nitrogen atoms in the
atmosphere to produce 14C.
The 14C formed in this reaction is a neutron-rich nuclide that decays by electron emission with a half-life of 5730 years.
Just after World War II, Willard F. Libby proposed a way to use these reactions to estimate the age of carbon-containing substances. The 14C dating technique for which Libby received the Nobel prize was based on the following assumptions.
- 14C is produced in the atmosphere at a more or less constant rate.
- Carbon atoms circulate between the atmosphere, the oceans, and living organisms at a rate very much faster than they decay. As a result, there is a constant concentration of 14C in all living things.
- After death, organisms no longer pick up 14C.
Thus, by comparing the activity of a sample with the activity of living tissue we can estimate how long it has been since the organism died.
The natural abundance of 14C is about 1 part in 1012 and the average activity of living tissue is 15.3 disintegrations per minute per gram of carbon. Samples used for 14C dating can include charcoal, wood, cloth, paper, sea shells, limestone, flesh, hair, soil, peat, and bone. Since most iron samples also contain carbon, it is possible to estimate the time since iron was last fired by analyzing for 14C.
| Practice Problem 9: The skin, bones and clothing of an adult female mummy discovered in Chimney Cave, Lake Winnemucca, Nevada, were dated by radiocarbon analysis. How old is this mummy if the sample retains 73.9% of the activity of living tissue? |
We now know that one of Libby's assumptions is questionable: The amount of 14C in the atmosphere hasn't been constant with time. Because of changes in solar activity and the earth's magnetic field, it has varied by as much as 5%. More recently, contamination from the burning of fossil fuels and the testing of nuclear weapons has caused significant changes in the amount of radioactive carbon in the atmosphere. Radiocarbon dates are therefore reported in years before the present era (B.P.). By convention, the present era is assumed to begin in 1950, when 14C dating was introduced.
Studies of bristlecone pines allow us to correct for changes in the abundance of 14C with time. These remarkable trees, which grow in the White Mountains of California, can live for up to five thousand years. By studying the 14C activity of samples taken from the annual growth rings in these trees, researchers have developed a calibration curve for 14C dates from the present back to 5145 B.C.
After roughly 45,000 years (eight half-lives), a sample retains only 0.4% of the 14C activity of living tissue. At that point it becomes too old to date by radiocarbon techniques. Other radioactive isotopes can be used to date rocks, soils, or archaeological objects that are much older. Potassium-argon dating, for example, has been used to date samples up to 4.3 billion years old. Naturally occurring potassium contains 0.0118% by weight of the radioactive 40K isotope. This isotope decays to 40Ar with a half-life of 1.3 billion years. The 40Ar produced after a rock crystallizes is trapped in the crystal lattice. It can be released, however, when the rock is melted at temperatures up to 2000C. By measuring the amount of 40Ar released when the rock is melted and comparing it with the amount of potassium in the sample, the time since the rock crystallized can be determined.