| Definition of Work | Heat and Work | Conservation of Energy | Internal Energy |
| Interconversion of Heat and Work | State Functions | Calorimeter | |
Work can be defined as the product of the force used to move an object times the distance the object is moved.
w = F x d
| Practice Problem 2: Calculate the amount of work that has to be done to lift a 10-pound bag of groceries a distance of 2.5 feet from the floor to the top of the kitchen counter. |
Imagine a system that consists of a sample of ammonia trapped in a piston and cylinder, as shown in the figure below. Assume that the pressure of the gas pushing up on the piston just balances the weight of the piston, so that the volume of the gas is constant. Now assume that the gas decomposes to form nitrogen and hydrogen, increasing the number of gas particles in the container. If the temperature and pressure of the gas are held constant, this means that the volume of the gas must increase.
2 NH3(g) ![]() N2(g) + 3 H2(g)
N2(g) + 3 H2(g)

The volume of the gas can increase by pushing the piston partway out of the cylinder. The amount of work done is equal to the product of the force exerted on the piston times the distance the piston is moved.
w = F x d
The pressure (P) the gas exerts on the piston is equal to the force (F) with which it pushes up on the piston divided by the surface area (A) of the piston.

Thus, the force exerted by the gas is equal to the product of its pressure times the surface area of the piston.
F = P x A
Substituting this expression into the equation defining work gives the following result.
w = (P x A) x d
The product of the area of the piston times the distance the piston moves is equal to
the change that occurs in the volume of the system when the gas expands. By convention,
the change in the volume is represented by the symbol ![]() V.
V.
![]() V
= A x d
V
= A x d
The magnitude of the work done when a gas expands is therefore equal to the product of the pressure of the gas times the change in the volume of the gas.
|w| = P![]() V
V
The Joule - Measuring Heat and Work
By definition, one joule is the work done when a force of one newton is used to move an object one meter.
1 J = 1 N-m
Because work can be converted into heat and vice versa, the SI system uses the joule to measure energy in the form of both heat and work.
The First Law of Thermodynamics: Conservation of Energy
The first law of thermodynamics states that energy cannot be created or destroyed. A system can gain or lose energy. But any change in the energy of the system must be accompanied by an equivalent change in the energy of its surroundings because the total energy of the universe is constant. The first law of thermodynamics can be described by the following equation.
![]() Euniv
=
Euniv
= ![]() Esys
+
Esys
+ ![]() Esurr
= 0
Esurr
= 0
(The subscripts univ, sys, and surr stand for the universe, the system and its surroundings.)
The energy of a system is often called its internal energy because it is the sum of the kinetic and potential energies of the particles that form the system. Because there is no interaction between particles, the only contribution to the internal energy of an ideal gas is the kinetic energy of the particles. The internal energy of an ideal gas is therefore directly proportional to the temperature of the gas.

(In this equation, R is the ideal gas constant and T is the temperature of the gas in units of Kelvin.)
Although it is difficult, if not impossible, to write an equation for more complex systems, the internal energy of the system is still directly proportional to its temperature. We can therefore use changes in the temperature of a system to monitor changes in its internal energy.
The magnitude of the change in the internal energy of a system is defined as the difference between the initial and final values of this quantity.
![]() Esys
= Efinal - Einitial
Esys
= Efinal - Einitial
Because the internal energy of a system is proportional to its temperature, ![]() E
is positive when the temperature of the system increases.
E
is positive when the temperature of the system increases.
The First Law of Thermodynamics: Interconversion of Heat and Work
Energy can be transferred between a system and its surroundings as long as the energy gained by one of these components of the universe is equal to the energy lost by the other.
![]() Esys
= -
Esys
= - ![]() Esurr
Esurr
Energy can be transferred between a system and its surroundings in the form of either heat (q) or work (w).
![]() Esys
= q + w
Esys
= q + w
When heat enters a system it can increase the temperature of the system or it can do work.
q = ![]() Esys
- w
Esys
- w
The sign convention for the relationship between the internal energy of a system and the heat that crosses the boundary between the system and its surroundings is given in the figure below.
- When the heat that enters a system increases the temperature of the system, the internal
energy of the system increases, and
 E
is positive.
E
is positive. - When the temperature of the system decreases because heat leaves the system,
 E
is negative.
E
is negative.
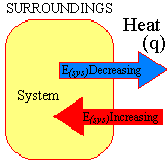
The sign convention for the relationship between work and the internal energy of a system is shown on the left side of the figure below.
- When the system does work on its surroundings, energy is lost, and
 E
is negative.
E
is negative. - When the surroundings do work on the system, the internal energy of the system becomes
larger, so
 E
is positive.
E
is positive.

The relationship between the magnitude of the work done by a system when it expands and the change in the volume of the system was previously described by the following equation.
|w| = P![]() V
V
The figure above shows that the sign convention for work of expansion can be included by writing this equation as follows.
w = - P![]() V
V
When equations connect two or more properties that describe the state of the system, they are called equations of state. The ideal gas law, for example, is an equation of state.
PV = nRT
State functions depend only on the state of the system, not on the path used to get to that state.
Temperature is a state function. No matter how many times we heat, cool, expand, compress, or otherwise change the system, the net change in the temperature only depends on the initial and final states of the system.
![]() T
= Tfinal - Tinitial
T
= Tfinal - Tinitial
The same can be said for the volume, pressure, and the number of moles of gas in the sample. These quantities are all state functions.
Heat and work are not state functions. Work can't be a state function because it is proportional to the distance an object is moved, which depends on the path used to go from the initial to the final state. If work isn't a state function, then heat can't be a state function either. According to the first law of thermodynamics, the change in the internal energy of a system is equal to the sum of the heat and the work transferred between the system and its surroundings.
![]() Esys
= q + w
Esys
= q + w
If ![]() E
does not depend on the path used to go from the initial to the final state, but the amount
of work does depend on the path used, the amount of heat given off or absorbed must depend
on the path.
E
does not depend on the path used to go from the initial to the final state, but the amount
of work does depend on the path used, the amount of heat given off or absorbed must depend
on the path.
The thermodynamic properties of a system that are state functions are usually symbolized by capital letters (T, V, P, E, and so on). Thermodynamic properties that are not state functions are often described by lowercase letters (q and w).
| Practice Problem 3: Which of the following properties of a gas are state functions? (a) Temperature, T (b) Volume, V (c) Pressure, P (d) Number of moles of gas, n (e) Internal energy, E |
Measuring Heat with a Calorimeter
The amount of heat given off or absorbed in a chemical reaction can be measured with a calorimeter like the one shown in the figure below.

Because the reaction occurs in a sealed container at constant volume, no work of expansion is done during the reaction. The heat given off or absorbed by the reaction is therefore equal to the change in the internal energy of the system during the course of the reaction:
![]() Esys
= qV.
Esys
= qV.
The amount of heat given off or absorbed by the water in a calorimeter can be calculated from the heat capacity of water.

| Practice Problem 4: The natural gas in methane reacts with oxygen to give carbon dioxide and water. CH4(g) + 2 O2(g) Calculate the heat given off when 0.160 g of methane reacts with excess oxygen in a bomb calorimeter if the temperature of the 1.000 kg of water in the bath surrounding the bomb increases by 1.918oC. |
Heat is an extensive quantity. The most common approach for converting a measurement of heat into an intensive quantity is to calculate the heat of reaction in units of kilojoules per mole. The result of this calculation is a quantity known as the molar heat of reaction. By definition, the molar heat of reaction is the heat given off or absorbed by the reaction expressed in units of kilojoules per mole of one of the reagents in the reaction.
