The valence-bond model and the crystal field theory explain some aspects of the chemistry of the transition metals, but neither model is good at predicting all of the properties of transition-metal complexes. A third model, based on molecular orbital theory, was therefore developed that is known as ligand-field theory. Ligand-field theory is more powerful than either the valence-bond or crystal-field theories. Unfortunately it is also more abstract.

The ligand-field model for an octahedral transition-metal complex such as the Co(NH₃)₆³⁺ ion assumes that the 3d, 4s, and 4p orbitals on the metal overlap with one orbital on each of the six ligands to form a total of 15 molecular orbitals, as shown in the figue below.

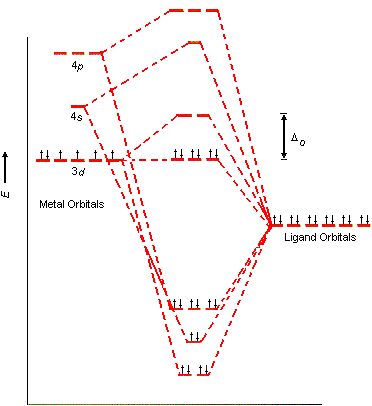
Six of these orbitals are bonding molecular orbitals, whose energies are much lower than those of the original atomic orbitals. Another six are antibonding molecular orbitals, whose energies are higher than those of the original atomic orbitals. Three are best described as nonbonding molecular orbitals, because they have essentially the same energy as the 3d atomic orbitals on the metal.

Ligand-field theory enables the 3d, 4s, and 4p orbitals on the metal to overlap with orbitals on the ligand to form the octahedral covalent bond skeleton that holds this complex together. At the same time, this model generates a set of five orbitals in the center of the diagram that are split into t_2g and e_g subshells, as predicted by the crystal-field theory. As a result, we don't have to worry about "inner-shell" versus "outer-shell" metal complexes. In effect, we can use the 3d orbitals in two different ways. We can use them to form the covalent bond skeleton and then use them again to form the orbitals that hold the electrons that were originally in the 3d orbitals of the transition metal.