The Structure of Metals and Other Monatomic Solids
The structures of pure metals are easy to describe because the atoms that form these metals can be thought of as identical perfect spheres. The same can be said about the structure of the rare gases (He, Ne, Ar, and so on) at very low temperatures. These substances all crystallize in one of four basic structures: simple cubic (SC), body-centered cubic (BCC), hexagonal closest-packed (HCP), and cubic closest-packed (CCP).
When a solid crystallizes, the particles that form the solid pack as tightly as possible. To illustrate this principle, let's try to imagine the best way of packing spheres, such as ping-pong balls, into an empty box.
One approach involves carefully packing the ping-pong balls to form a square packed plane of spheres, as shown in the figure below.
By tilting the box to one side, we can stack a second plane of spheres directly on top of the first. The result is a regular structure in which the simplest repeating unit is a cube of eight spheres, as shown in the figure below.
This structure is called simple cubic packing. Each sphere in this structure touches four identical spheres in the same plane. It also touches one sphere in the plane above and one in the plane below. Each atom in this structure can form bonds to its six nearest neighbors. Each sphere is therefore said to have a coordination number of 6.
A simple cubic structure is not an efficient way of using
space. Only 52% of the available space is actually occupied by
the spheres in a simple cubic structure. The rest is empty space.
Because this structure is inefficient, only one element![]() polonium
polonium![]() crystallizes
in a simple cubic structure.
crystallizes
in a simple cubic structure.
Another approach starts by separating the spheres to form a square-packed plane in which they do not quite touch each other, as shown in the figure below.
The spheres in the second plane pack above the holes in the first plane, as shown in the figure below.
Spheres in the third plane pack above holes in the second plane. Spheres in the fourth plane pack above holes in the third plane, and so on. The result is a structure in which the odd-numbered planes of atoms are identical and the even-numbered planes are identical. This ABABABAB. . . repeating structure is known as body-centered cubic packing.
This structure is called body-centered cubic because
each sphere touches four spheres in the plane above and four more
in the plane below, arranged toward the corners of a cube. Thus,
the repeating unit in this structure is a cube of eight spheres
with a ninth identical sphere in the center of the body![]() in
other words, a body-centered cube, as shown in the figure below.
The coordination number in this structure is 8.
in
other words, a body-centered cube, as shown in the figure below.
The coordination number in this structure is 8.
Examine the Body-Centered Cubic Crystal below:
Press the left mouse button and drag over the structure. Press the right mouse button to see options.
This page requires the MDL Chime plugin. Download it here.
Body-centered cubic packing is a more efficient
way of using space than simple cubic packing![]() 68%
of the space in this structure is filled. All of the metals in
Group IA (Li, Na, K, and so on), the heavier metals in Group IIA
(Ca, Sr, and Ba), and a number of the early transition metals
(such as Ti, V, Cr, Mo, W, and Fe) pack in a body-centered cubic
structure.
68%
of the space in this structure is filled. All of the metals in
Group IA (Li, Na, K, and so on), the heavier metals in Group IIA
(Ca, Sr, and Ba), and a number of the early transition metals
(such as Ti, V, Cr, Mo, W, and Fe) pack in a body-centered cubic
structure.
Two structures pack spheres so efficiently they are called closest-packed structures.
Both start by packing the spheres in planes in which each sphere touches six others oriented toward the corners of a hexagon, as shown in figure the figure below.

A second plane is then formed by packing spheres above the triangular holes in the first plane, as shown in the figure below.
The spheres in the third plane could pack directly above the spheres in the first plane to form an ABABABAB. . . repeating structure. Because this structure is composed of alternating planes of hexagonal closest-packed spheres, it is called a hexagonal closest-packed structure. Each sphere touches three spheres in the plane above, three spheres in the plane below, and six spheres in the same plane, as shown in the figure below. Thus, the coordination number in a hexagonal closest-packed structure is 12.

74% of the space in a hexagonal closest-packed structure is filled. No more efficient way of packing spheres is known, and the hexagonal closest-packed structure is important for metals such as Be, Co, Mg, and Zn, as well as the rare gas He at low temperatures.
There is another way of stacking hexagonal closest-packed planes of spheres. The atoms in the third plane can be packed above the holes in the first plane that were not used to form the second plane. The fourth hexagonal closest-packed plane of atoms then packs directly above the first. The net result is an ABCABCABC. . . structure, which is called cubic closest-packed. Each sphere in this structure touches six others in the same plane, three in the plane above, and three in the plane below, as shown in the figure below. Thus, the coordination number is still 12.

The difference between hexagonal and cubic closest-packed structures can be understood by noting that the atoms in the first and third planes lie directly above each other in a hexagonal closest-packed structure. In the cubic closest-packed structure, the atoms in these planes are oriented in different directions.
The cubic closest-packed structure is just as efficient as the hexagonal closest packed structure. (Both use 74% of the available space.) Many metals, including Ag, Al, Au, Ca, Co, Cu, Ni, Pb, and Pt, crystallize in a cubic closest-packed structure. So do all the rare gases except helium when these gases are cooled to low enough temperatures to solidify.
The face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure. In fact, the presence of face-centered cubic unit cells in this structure explains why the structure is known as cubic closest-packed.
Coordination Numbers and the Structures of Metals
The coordination numbers of the four structures of metals are summarized in the table below. It is easy to understand why metals pack in hexagonal or cubic closest-packed structures. Not only do these structures use space as efficiently as possible, they also have the largest possible coordination numbers, which allows each metal atom to form bonds to the largest number of neighboring metal atoms.
Coordination Numbers for Common Crystal Structures
| Structure | Coordination Number |
Stacking Pattern |
||
| simple cubic | 6 | AAAAAAAA. . . | ||
| body-centered cubic | 8 | ABABABAB. . . | ||
| hexagonal closest-packed | 12 | ABABABAB. . . | ||
| cubic closest-packed | 12 | ABCABCABC. . . |
It is less obvious why one-third of the metals pack in a body-centered cubic structure, in which the coordination number is only 8. The popularity of this structure can be understood by referring to the figure below.
The coordination number for body-centered cubic
structures given in the table above counts only the atoms that
actually touch a given atom in this structure. The figure above
shows that each atom also almost touches four neighbors in
the same plane, a fifth neighbor two planes above, and a sixth
two planes below. The distance from each atom to the nuclei of
these nearby atoms is only 15% larger than the distance to the
nuclei of the atoms that it actually touches. Each atom in a
body-centered cubic structure therefore can form a total of 14
bonds ![]() eight strong bonds to the atoms that it touches and six weaker
bonds to the atoms it almost touches.
eight strong bonds to the atoms that it touches and six weaker
bonds to the atoms it almost touches.
This makes it easier to understand why a metal might prefer the body-centered cubic structure to the hexagonal or cubic closest-packed structure. Each metal atom in the closest-packed structures can form strong bonds to 12 neighboring atoms. In the body-centered cubic structure, each atom forms a total of 14 bonds to neighboring atoms, although six of these bonds are somewhat weaker than the other eight.
Physical Properties that Result from the Structure of Metals
The structures of metals can be used to explain many of the characteristic physical properties of metals.
When asked to explain why metals have a characteristic metallic shine, or luster, many people would say that metals reflect (literally, throw back) the light that shines on their surface. They might argue, in effect, that light bounces off a metal's surface the way a racquetball bounces off the walls of a racquetball court. There is something wrong with this analogy, however. Metals actually absorb a significant fraction of the light that hits their surface.
A portion of the energy captured when the metal
absorbs light is turned into thermal energy. (You can easily
demonstrate this by placing your hand on the surface of a car
that has spent several hours in the sun.) The rest of the energy
is reradiated by the metal as "reflected" light. Silver
is better than any other metal at reflecting light, and yet only
88% of the light that hits the surface of a silver mirror is
reradiated. This raises an important question: Why do metals
absorb light when other substances, such as the glass in the
car's windows, do not? Light is absorbed when the energy of this
radiation is equal to the energy needed to excite an electron to
a higher-energy excited state or when the energy can be used to
move an electron through the solid. Because electrons are
delocalized in metals![]() and
therefore free to move through the solid
and
therefore free to move through the solid![]() metals
absorb light easily. Other solids, such as glass, don't have
electrons that can move through the solid, so they can't absorb
light the way metals do. These solids are colorless and can only
be colored by adding an impurity in which the energy associated
with exciting an electron from one orbital to another falls in
the visible portion of the spectrum. Glass is usually colored by
adding a small quantity of one of the transition metals. Cobalt
produces a blue color, chromium makes the glass appear green, and
traces of gold give a deep-red color.
metals
absorb light easily. Other solids, such as glass, don't have
electrons that can move through the solid, so they can't absorb
light the way metals do. These solids are colorless and can only
be colored by adding an impurity in which the energy associated
with exciting an electron from one orbital to another falls in
the visible portion of the spectrum. Glass is usually colored by
adding a small quantity of one of the transition metals. Cobalt
produces a blue color, chromium makes the glass appear green, and
traces of gold give a deep-red color.
Why are metals solid? Nonmetals such as hydrogen and oxygen are gases at room temperature because these elements can achieve a filled shell of valence electrons by sharing pairs of electrons to form relatively small molecules, such as H2 and O2, that are moving fast enough at room temperature to escape from the liquid into the gaseous phase. Metals can't do this. There aren't enough electrons on a metal atom to allow it to fill its valence shell by sharing pairs of electrons with one or two nearest neighbors. The only way a metal can obtain the equivalent of a filled shell of valence electrons is by allowing these electrons to be shared by a number of adjacent metal atoms. This is possible only if a large number of metal atoms are kept close together, and metals are therefore solids at room temperature.
Why are metals malleable and ductile? Most metals pack in either body-centered cubic, hexagonal closest-packed, or cubic closest-packed structures. In theory, changing the shape of the metal is simply a matter of applying a force that makes the atoms in one of the planes slide past the atoms in an adjacent plane, as shown in the figure below. In practice, it is easier to do this when the metal is hot.

Why are metals good conductors of heat and electricity? As we have already seen, the delocalization of valence electrons in a metal allows the solid to conduct an electric current. To understand why metals conduct heat, remember that temperature is a macroscopic property that reflects the kinetic energy of the individual atoms or molecules. The tight packing of atoms in a metal means that kinetic energy can be transferred from one atom to another both rapidly and efficiently.
Solid Solutions and Intermetallic Compounds
Most of the solutions chemists work with involve a gas (such as HCl) or a solid (such as NaCl) dissolved in a liquid (such as water). It is also possible to prepare solutions in which a gas, a liquid, or a solid dissolves in a solid. The most important class of solid solutions are those in which one solid is dissolved in another. Two examples of solid solutions are copper dissolved in aluminum and carbon dissolved in iron.
The solubility of one solid in another usually depends on temperature. At room temperature, for example, copper doesn't dissolve in aluminum. At 550C, however, aluminum can form solutions that contain up to 5.6% copper by weight. Aluminum metal that has been saturated with copper at 550C will try to reject the copper atoms as it cools to room temperature. In theory, the solution could reject copper atoms by forming a polycrystalline structure composed of small crystals of more or less pure aluminum interspersed with small crystals of copper metal. Instead of this, the copper atoms combine with aluminum atoms as the solution cools to form an intermetallic compound with the formula CuAl2.
CuAl2 is a perfect example of the
difference between a mixture (such as a solution of copper
dissolved in aluminum) and a compound. The solution can contain
varying amounts of copper and aluminum. At 550C, for example,
the solution can contain between 0 and 5.6% copper metal by
weight. The intermetallic compound has a fixed composition ![]() CuAl2
is always 49.5% aluminum by weight.
CuAl2
is always 49.5% aluminum by weight.
Intermetallic compounds such as CuAl2 are the key to a process known as precipitation hardening. Aluminum metal packs in a cubic closest-packed structure in which one plane of atoms can slip past another. As a result, pure aluminum metal is too weak to be used as a structural metal in cars or airplanes. Precipitation hardening produces alloys that are five to six times as strong as aluminum, and make an excellent structural metal.
The first step in precipitation hardening of aluminum involves heating the metal to 550C. Copper is then added to form a solution, which is quenched with cold water. The solution cools so fast that the copper atoms can't come together to form microcrystals of copper metal.
Comparing a solid with a brick wall has one major disadvantage. It leads one to believe that atoms can't move through the metal. This is not quite true. Diffusion through the metal can occur, although it occurs slowly. Over a period of time, copper atoms can move through the quenched solution to form microcrystals of the CuAl2 intermetallic compound that are so small they are hard to see with a microscope.
These CuAl2 particles are both hard and strong. So hard they inhibit the flow of the aluminum metal that surrounds them. These microcrystals of CuAl2 strengthen aluminum metal by interfering with the way planes of atoms slip past each other. The result is a metal that is both harder and stronger than pure aluminum.
Copper dissolved in aluminum at high temperature is an example of a substitution solution, in which copper atoms pack in the positions normally occupied by aluminum atoms. There is another way in which a solid solution can be made. Atoms of one element can pack in the holes, or interstices, between atoms of the host element because even the most efficient crystal structures use only 74% of the available space in the crystal. The result is an interstitial solution.
Steel at high temperatures is a good example of an interstitial solution. Steel is formed by dissolving carbon in iron. At very high temperatures, iron packs in a cubic closest-packed structure that leaves just enough space to allow carbon atoms to fit in the holes between the iron atoms. Below 910C, iron metal packs in a body-centered cubic structure, in which the holes are too small to hold carbon atoms.
This has important consequences for the
properties of steel. At temperatures above 910C, carbon readily
dissolves in iron to form a solid solution that contains as much
as 1% carbon by weight. This material is both malleable and
ductile, and it can be rolled into thin sheets or hammered into
various shapes. When this solution cools below 910C, the iron
changes to a body-centered cubic structure, and the carbon atoms
are rejected from the metal. If the solution is allowed to cool
gradually, the carbon atoms migrate through the metal to form a
compound with the formula Fe3C, which precipitates
from the solution. These Fe3C crystals serve the same
role in steel that the CuAl2 crystals play in aluminum![]() they
inhibit the flow of the planes of metal atoms and thereby make
the metal stronger.
they
inhibit the flow of the planes of metal atoms and thereby make
the metal stronger.
Holes in Closest-Packed and Simple Cubic Structures
Metals aren't the only solids that pack in simple cubic, body-centered cubic, hexagonal closest-packed, and cubic closest-packed structures. A large number of ionic solids use these structures as well.
Sodium chloride (NaCl) and zinc sulfide (ZnS), for example, form crystals that can be thought of as cubic closest-packed arrays of negative ions (Cl- or S2-), with positive ions (Na+ or Zn2+) packed in holes between the closest-packed planes of negative ions. There is a subtle difference between these structures, however, because the Na+ ions in NaCl pack in holes that are different from those used by the Zn2+ ions in ZnS.
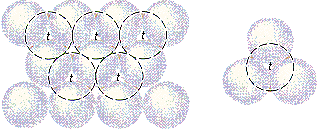
There are two kinds of holes in a closest-packed structure. So-called tetrahedral holes are shown in the figure below. The solid lines in this figure represent one plane of closest-packed atoms. The dashed lines represent a second plane of atoms, which pack above the holes in the first plane. Each of the holes marked with a t touches three atoms in the first plane and one atom in the second plane. They are called tetrahedral holes because positive ions that pack in these holes are surrounded by four negative ions arranged toward the corners of a tetrahedron.
The octahedral holes in a closest-packed structure are shown in the figure below. Once again, the solid lines represent one plane of closest-packed atoms and the dashed lines correspond to a second plane, which packs above the holes in the first plane. Each of the holes marked with an o touches three atoms in the first plane and three atoms in the second plane. They are called octahedral holes because positive ions that occupy these holes are surrounded by six negative ions arranged toward the corners of an octahedron.
Tetrahedral holes are very small. The largest atom that can fit into a tetrahedral hole without distorting the tetrahedron has a radius only 0.225 times the radius of the atoms that form the hole. Octahedral holes are almost twice as large as tetrahedral holes. The largest atom that can fit into an octahedral hole has a radius 0.414 times the radius of the atoms that form the hole. The relative size of the atoms or ions that form a crystal therefore dictates whether tetrahedral or octahedral holes are used.
Sometimes positive ions are too big to pack in either tetrahedral or octahedral holes in a closest-packed structure of negative ions. When this happens, the negative ions pack in a simple cubic structure, and the positive ions pack in cubic holes between the planes of negative ions.
The discussion of tetrahedral, octahedral, and cubic holes in the previous section suggests that the structure of an ionic solid depends on the relative size of the ions that form the solid. The relative size of these ions is given by the radius ratio, which is the radius of the positive ion divided by the radius of the negative ion.
![]()
The relationship between the coordination number of the positive ions in ionic solids and the radius ratio of the ions is given in the table below. As the radius ratio increases, the number of negative ions that can pack around each positive ion increases. When the radius ratio is between 0.225 and 0.414, positive ions tend to pack in tetrahedral holes between planes of negative ions in a cubic or hexagonal closest-packed structure. When the radius ratio is between 0.414 and 0.732, the positive ions tend to pack in octahedral holes between planes of negative ions in a closest-packed structure.
Radius Ratio Rules
| Radius Ratio |
Coordination Number |
Holes in Which Positive Ions Pack |
||
| 0.225 - 0.414 | 4 | tetrahedral holes | ||
| 0.414 - 0.732 | 6 | octahedral holes | ||
| 0.732 - 1 | 8 | cubic holes | ||
| 1 | 12 | closest-packed structure |
The table above suggests that tetrahedral holes aren't used until the positive ion is large enough to touch all four of the negative ions that form this hole. As the radius ratio increases from 0.225 to 0.414, the positive ion distorts the structure of the negative ions toward a structure that purists might describe as closely-packed.
As soon as the positive ion is large enough to touch all six negative ions in an octahedral hole, the positive ions start to pack in octahedral holes. These holes are used until the positive ion is so large that it can't fit into even a distorted octahedral hole.
Eventually a point is reached at which the positive ion can no longer fit into either the tetrahedral or octahedral holes in a closest-packed crystal. When the radius ratio is between about 0.732 and 1, ionic solids tend to crystallize in a simple cubic array of negative ions with positive ions occupying some or all of the cubic holes between these planes. When the radius ratio is about 1, the positive ions can be incorporated directly into the positions of the closest-packed structure.
| Practice Problem 1: The following compounds have similar empirical formulas. Use the radius ratio rules and the table of ionic radii in the appendix to explain why they have different structures. (a) NaCl (b) ZnS (c) CsCl |
The structure of ionic solids is also affected by differences in the abundance of tetrahedral and octahedral holes in a closest-packed structure. There are just as many octahedral holes as there are spheres that form the closest-packed structure. Thus, if NaCl is a 1:1 salt in which the Na+ ions occupy octahedral holes in a closest-packed array of Cl- ions, all of the octahedral holes in this structure must be filled.
There are twice as many tetrahedral holes in a closest-packed structure. The Zn2+ ions in ZnS therefore occupy only half of the tetrahedral holes in a closest-packed array of S2- ions.