Nuclear Synthesis and Nuclear Medicine
Within the last 60 years, scientists have generated a new story of creation that offers a model for understanding how nuclei are synthesized.
In 1929, Edwin Hubble provided evidence to suggest that our universe is expanding. Between 1946 and 1948, George Gamow and co-workers generated a model which assumed that the primordial substance, or ylem, from which all other matter was created was an extraordinarily hot, dense singularity that exploded in a "Big Bang" and has been expanding ever since. This model assumes that neutrons in the ylem were transformed into protons by �/i>-decay. Neutrons and protons then combined to form 4He atoms before the temperature and pressure of the fireball decayed to the point at which no further nuclear reactions were possible.
The first-generation stars condensed out of this cloud of hydrogen and helium. As the gas condensed by gravitational attraction, it became warmer. Eventually, the temperature reached 107 K, and first-generation, main-sequence stars were born. The temperature at the cores of these stars was high enough to ignite the following thermonuclear reactions.
The net result of these reactions is the formation of a helium atom from four protons.
Eventually the heat generated in this reaction was enough to halt the gravitational collapse of the star, which entered a stable period during which the energy generated by this reaction balanced the energy radiated at the surface.
The hydrogen-burning reactions in a main-sequence star are concentrated in the core. When enough hydrogen has been consumed, the core begins to collapse, and the temperature of the core rises above 108 K. (The larger the star, the more rapidly it radiates energy from its surface, and the more rapidly it consumes the hydrogen in the core.) As the core collapses, the hydrogen-containing outer shell expands, and the surface of the star cools. Stars that have reached this point in their evolution include the so-called red giants.
Temperatures in the core of these red giants are high enough to ignite further thermonuclear fusion reactions, such as the following.
This reaction becomes the principal source of energy in a red giant, although there is undoubtedly some burning of hydrogen to helium in the outer shell of the star. As the amount of 12C in the core increases, further reactions occur to form 16O and 20Ne.
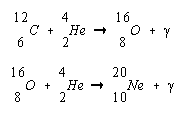
Eventually, the helium in the core is exhausted, and the core collapses further, reaching temperatures of 6-7 x 108 K. At this point, more complex reactions take place that produce nuclides such as 28Si and 32S.
Further gravitational collapse heats the core to temperatures above 109 K, and a complex sequence of reactions takes place to synthesize the nuclei with the highest binding energies, such as Fe and Ni. If the star explodes in a supernova, its contents are ejected across space. Second-generation stars that condense in this region contain not only hydrogen and helium but elements with higher atomic number.
The best estimates of the age of the Milky Way suggest that our galaxy is about 15 billion years old. Our sun and its planets, however, are only 4.6 billion years old. This suggests that the sun is a second-generation star. In such stars, the transformation of hydrogen to helium can be catalyzed by 12C, as shown in the figure below.
 |
| Second-generation stars use a different mechanism to synthesis helium than first-generation stars. They use a sequence of reactions, such as the those shown here, that are catalyzed by isotopes heavier than helium. |
Two processes can synthesize elements with atomic numbers
larger than that of iron. One of them is relatively slow (s-process), the other is very
rapid (r-process). Since the only way to synthesize nuclei with atomic numbers larger than
iron is by the absorption of neutrons, both the s-process and the r-process result from
(n,
) reactions.
In the s-process, neutrons are captured one at a
time to form a neutron-rich nuclide that has enough time to undergo 
- or �sup>--decay
before another neutron can be absorbed. An example of an s-process sequence of reactions
starts with 120Sn. The capture of a neutron produces 121Sn, which
undergoes �/i>--decay. If �/i>--decay occurs before this
nuclide captures another neutron, a stable isotope of antimony is formed. Eventually, 121Sb
captures a neutron to produce 122Sb, which is transformed into 122Te
by �/i>-decay. 122Te can undergo �/i>--decay to form 122I,
or it can capture a neutron to form 123Te. With 123Te, we encounter
a series of stable isotopes of tellurium. Thus, neutrons are slowly absorbed, one at a
time, until we reach 127Te, which decays to 127I, the most abundant
isotope of iodine.
This slow process can't account for very heavy nuclides,
such as 232Th and 238U, because the lifetimes of the intermediate
nuclei with atomic numbers between 83 and 90 are too short for this step-by-step
absorption of neutrons to proceed. Synthesizing appreciable quantities of uranium and
thorium requires a rapid process. In the r-process, a number of neutrons are
captured in rapid succession, before there is time for - or �/i>-decay to take place. Achieving an
r-process reaction, however, requires a very high neutron flux. (These reactions occur
during nuclear explosions, for example.) The neutron flux needed to fuel such reactions is
not likely to occur in a normal star. During the moment when a star explodes as a
supernova, however, the conditions are ripe for r-process reactions. The heavier elements
on this planet were therefore produced in a series of supernova explosions that occurred
in this portion of the galaxy before our solar system condensed.
Ever since the first x-ray images were obtained by Roentgen in 1895, ionizing radiation and radionuclides have played a vital role in medicine. This work has been so fruitful that a separate field known as nuclear medicine has developed. Research in this field focuses on either therapeutic or diagnostic uses of radiation.
There are three standard approaches to fighting cancer: surgery, chemotherapy, and radiation. Surgery, by its very nature, is invasive. Chemotherapy and classic approaches to radiation therapy are not selective. Research in recent years has therefore examined new approaches to radiation therapy that specifically attack tumor cells, without damaging normal tissue. The technique known as boron neutron capture therapy provides an example of this work [R. F. Barth, A. H. Soloway, and R. G. Fairchild, Cancer Research, 50, 1061 (1990)].
Naturally occurring boron consists of two stable isotopes:
10B (19.7%) and 11B (80.3%). 10B absorbs thermal neutrons
to form 11B in a nuclear excited state. Although 11B in its nuclear
ground state is stable, this excited 11B nuclide undergoes fission to produce 7Li
and an -particle.
Because the energy of a thermal neutron is only about
0.025 eV, the neutrons that are not absorbed do relatively little damage to the normal
tissue. The -particle
emitted in this reaction has an energy of 2.79 MeV, however, which makes it an extremely
lethal form of radiation. The RBE for -particle radiation is larger than most other particles because
this relatively massive particle loses energy very efficiently as it collides with matter.
Radiation damage from the -particle is therefore restricted to the immediate vicinity of the tissue
that absorbed the thermal neutron.
Although other common nuclides in living tissue can absorb thermal neutrons, the ability of 10B to absorb thermal neutrons is three orders of magnitude larger than these nuclides. The units with which this measurement is made can be understood by thinking about the area around the nuclide through which the neutron can pass and still be absorbed. The neutron-capture cross section for a hydrogen atom corresponds to a circle with a radius of about 2 x 10-13 cm. For a nitrogen atom, the radius of this circle is about 10-12 cm. Boron has a neutron-capture cross section that would be described by a circle with a radius of about 2 x 10-9 cm. Virtually all of the neutron capture that occurs is therefore concentrated in the tissue that contains boron.
The potential of boron neutron capture therapy was recognized as early as 1936. Early clinical trials in the late 1950s and early 1960s failed to prolong the lives of patients suffering from brain tumors because the boron compounds available for testing did not concentrate selectively in the tumor cells. Recent research has discovered boron-labeled compounds that are sufficiently selective for BNCT to become useful as an adjunct to surgery, or in place of surgery with inoperable cases.