The Structure of Metals

The structures of pure metals are easy to describe because the atoms can be thought of as identical perfect spheres. These substances all crystallize in one of four basic structures known as simple cubic (SC), body-centered cubic (BCC), hexagonal closest packed (HCP), and cubic closest packed (CCP).

The simplest structure to visualize is the one labeled simple cubic, in which the atoms form square packed planes, as shown in the figure below.

The second plane of atoms in this structure stacks directly on top of the first. The result is a regular structure in which the simplest repeating unit is a cube of eight spheres. Simple cubic structures aren't an efficient way of using space, only 52% of the available space is actually occupied by the spheres.

The first step toward a more efficient use of space is counterintuitive we separate the spheres to form a square packed plane in which they don't quite touch, as shown in the figure below.

Once this is done, the spheres in the second plane pack above the holes in the first plane, as shown in the figure below. Spheres in the third plane pack above holes in the second plane. Spheres in the fourth plane pack above holes in the third plane, and so on. The result is an ABABAB... repeating structure known as body-centered cubic packing.

Body-centered cubic packing is a more efficient way of using space than simple cubic packing

68% of the space in this structure is filled. As a result, body-centered cubic packing is an important structure for metals. All of the metals in Group IA (Li, Na, K, and so on), the heavier metals in Group IIA (Ca, Sr, and Ba), and a number of the early transition metals (such as Ti, V, Cr, Mo, W, and Fe) pack in a body-centered cubic structure.

Press the left mouse button and drag over the structure. Press the right mouse button to see options.

Two structures pack spheres so efficiently they are called closest packed structures.

Both start by packing the spheres in planes in which each sphere touches six others oriented toward the corners of a hexagon, as shown in the figure below.

A second plane is then formed by packing spheres above the triangular holes in the first plane.

The spheres in the third plane could pack directly above the spheres in the first plane to form an ABABAB. . . repeating structure known as hexagonal closest packing. Or the atoms in the third plane can pack above holes in the first plane that weren't used to form the second plane. This gives an ABCABCABC... repeating structure known as cubic closet packing. No more efficient way of packing spheres is known; 74% of the space is filled. Hexagonal closest packed structures are important for metals such as Be, Co, Mg, and Zn, as well as the rare gas He at low temperatures. Many metals, including Ag, Al, Au, Ca, Co, Cu, Ni, Pb, and Pt, crystallize in a cubic closest packed structure. So do all the rare gases except helium when these gases are cooled to low enough temperatures to solidify.

The difference between hexagonal and cubic closest packed structures can be understood by comparing the two figures below. In the hexagonal closest packed structure, the atoms in the first and third planes lie directly above each other.

Each atom in a hexagonal closest packed structure touches six atoms in the same plane, three in the plane above, and three in the plane below. The result is an ABABAB... repeating pattern of closest packed planes.

In the cubic closest packed structure, the atoms in these planes are oriented in different directions.

Each atom in a cubic closest packed structure touches six atoms in the same plane, three in the plane above, and three in the plane below. But the atoms in the top plane are rotated by 180 relative to the bottom plane to form an ABCABC... repeating pattern.

When asked to give an example of a solution, chemists usually think in terms of solutions of a gas such as HCl or a solid such as NaCl dissolved in a liquid such as water. It is also possible to prepare solutions in which one solid dissolves in another. The most important examples of these solid solutions are copper dissolved in aluminum and carbon dissolved in iron.

The solubility of one solid in another depends on temperature. At room temperature, copper doesn't dissolve in aluminum. But at 550ºC, aluminum can form solutions that contain up to 5.6% copper by weight. Aluminum metal that has been saturated with copper at 550C will try to reject the copper atoms as it cools to room temperature. In theory, the solution could reject copper atoms by forming a polycrystalline structure composed of small crystals of more or less pure aluminum interspersed with small crystals of copper metal. Instead of this, the copper atoms combine with aluminum atoms as the solution cools to form an intermetallic compound with the formula CuAl₂.

Intermetallic compounds such as CuAl₂ are the key to a process known as precipitation hardening. Aluminum metal packs in a cubic closest packed structure in which one plane of atoms can slip past another. As a result, pure aluminum metal is too weak to be used as a structural metal in cars or airplanes. Precipitation hardening produces alloys that are five to six times as strong as aluminum and make excellent structural metals.

The first step in precipitation hardening of aluminum involves heating the metal to 550ºC. Copper is then added to form a solution, which is quenched with cold water. The solution cools so fast that the copper atoms can't come together to form microcrystals of copper metal. Over a period of time, copper atoms can move through the quenched solution to form microcrystals of the CuAl₂ intermetallic compound that are so small they are hard to see with a microscope.

These CuAl₂ particles are both hard and strong. So hard they inhibit the flow of the aluminum metal that surrounds them. These microcrystals of CuAl₂ strengthen aluminum metal by interfering with the way planes of atoms slip past each other. The result is a metal that is both harder and stronger than pure aluminum.

Copper dissolved in aluminum at high temperature is an example of a substitution solution, in which copper atoms pack in the positions normally occupied by aluminum atoms. There is another way in which a solid solution can be made. Atoms of one element can pack in the holes, or interstices, between atoms of the host element because even the most efficient crystal structures use only 74% of the available space in the crystal. The result is an interstitial solution.

Steel at high temperatures is a good example of an interstitial solution. It is formed by dissolving carbon in iron. At very high temperatures, iron packs in a cubic closest packed structure that leaves just enough space to allow carbon atoms to fit in the holes between the iron atoms. Below 910ºC, iron metal packs in a body-centered cubic structure, in which the holes are too small to hold carbon atoms.

This has important consequences for the properties of steel. At temperatures above 910ºC, carbon readily dissolves in iron to form a solid solution that contains as much as 1% carbon by weight. This material is both malleable and ductile, and it can be rolled into thin sheets or hammered into various shapes. When this solution cools below 910ºC, the iron changes to a body-centered cubic structure, and the carbon atoms are rejected from the metal. If the solution is allowed to cool gradually, the carbon atoms migrate through the metal to form a compound with the formula Fe₃C, which precipitates from the solution. These Fe₃C crystals serve the same role in steel that the CuAl₂ crystals play in aluminum

they inhibit the flow of the planes of metal atoms and thereby make the metal stronger.

Metals aren't the only solids that pack in simple-cubic, body-centered cubic, hexagonal closest packed, and cubic closest packed structures. A large number of ionic solids use these structures as well.

Sodium chloride (NaCl) and zinc sulfide (ZnS), for example, form crystals that can be thought of as cubic closest packed arrays of negative ions (Cl^- or S^2-), with positive ions (Na⁺or Zn²⁺) packed in holes between the closest packed planes of negative ions. There is a subtle difference between these structures, however, because the Na⁺ ions in NaCl pack in holes that are different from those used by the Zn²⁺ions in ZnS.

There are two kinds of holes in a closest packed structure. The tetrahedral holes are shown in the figure below. The shaded spheres in this figure represent one plane of closest packed atoms. The dashed lines represent a second plane of atoms that pack above the holes in the first plane. Each of the holes marked with a t touches three atoms in the first plane and one atom in the second plane. They are called tetrahedral holes because positive ions that pack in these holes are surrounded by four negative ions arranged toward the corners of a tetrahedron.

The octahedral holes in a closest packed structure are shown in the figure below. Once again, the shaded spheres represent one plane of closest packed atoms and the dashed lines depict a second plane, which packs above the holes in the first plane. Each of the holes marked with an o touches three atoms in the plane below and three atoms in the plane above the hole. They are called octahedral holes because positive ions that occupy these holes are surrounded by six negative ions arranged toward the corners of an octahedron.

Tetrahedral holes are very small. The largest atom that can fit into a tetrahedral hole without distorting the tetrahedron has a radius only 0.225 times the radius of the atoms that form the hole. Octahedral holes are almost twice as large as tetrahedral holes. The largest atom that can fit into an octahedral hole has a radius 0.414 times the radius of the atoms that form the hole. The relative size of the atoms or ions that form a crystal therefore dictates whether tetrahedral or octahedral holes are used.

Sometimes positive ions are too big to pack in either tetrahedral or octahedral holes in a closest packed structure of negative ions. When this happens, the negative ions pack in a simple cubic structure, and the positive ions pack in cubic holes between the planes of negative ions.

The discussion of tetrahedral, octahedral, and cubic holes in the previous section suggests that the structure of an ionic solid depends on the relative size of the ions that form the solid. The relative size of these ions is given by the radius ratio, which is the radius of the positive ion divided by the radius of the negative ion.

The relationship between the coordination number of the positive ions in ionic solids and the radius ratio of the ions is given in the table below. As the radius ratio increases, the number of negative ions that can pack around each positive ion increases. When the radius ratio is between 0.225 and 0.414, positive ions tend to pack in tetrahedral holes between planes of negative ions in a cubic or hexagonal closest packed structure. When the radius ratio is between 0.414 and 0.732, the positive ions tend to pack in octahedral holes between planes of negative ions in a closest packed structure.

Radius Ratio	Coordination Number	Holes in which Positive Ions Pack
0.225-0.414	4	Tetrahedral holes
0.414-0.732	6	Octahedral holes
0.732-1	8	Cubic holes
1	12	Closest packed structure

The table above suggests that tetrahedral holes aren't used until the positive ion is large enough to touch all four of the negative ions that form this hole. As the radius ratio increases from 0.225 to 0.414, the positive ion distorts the structure of the negative ions toward a structure that might best be described as closely packed.

As soon as the positive ion is large enough to touch all six negative ions in an octahedral hole, the positive ions start to pack in these holes. These holes are used until the positive ion is so large that it can't fit into even a distorted octahedral hole.

Eventually a point is reached at which the positive ion can no longer fit into either the tetrahedral or octahedral holes in a closest packed crystal. When the radius ratio is between about 0.732 and 1, ionic solids tend to crystallize in a simple cubic array of negative ions with positive ions occupying some or all of the cubic holes between these planes. When the radius ratio is about 1, the positive ions can be incorporated directly into the closest packed structure.

The structure of ionic solids is also affected by differences in the abundance of tetrahedral and octahedral holes in a closest packed structure. There are just as many octahedral holes as there are spheres that form the closest packed structure. Thus, because NaCl is a 1: 1 salt in which the Na⁺ions occupy octahedral holes in a closest packed array of Cl^- ions, all of the octahedral holes in this structure must be filled.

There are twice as many tetrahedral holes as octahedral holes in a closest packed structure. The Zn²⁺ions in ZnS therefore occupy only half of the tetrahedral holes in a closest packed array of S^2-ions.

The simplest repeating unit in a crystal is called a unit cell. Each unit cell is defined in terms of lattice points the points in space about which the particles in a crystal are free to vibrate. In 1850, Auguste Bravais showed that crystals could be classified in terms of 14 unit cells, which meet the following criteria.

The 14 Bravais unit cells are shown in the figure below. These unit cells fall into seven categories that differ in the three unit-cell edge lengths (a, b, and c) and three internal angles (a,b , and g), as shown in the table below

Category	Edge Lengths	Internal Angles
Cubic	(a = b = c)	(a = ß = g = 90^o)
Tetragonal	(a = b c)	(a = ß = g = 90^o)
Monoclinic	(a b c)	(a = ß = 90^o g)
Orthorhombic	(a b c)	(a = ß = g = 90^o)
Rhombohedral	(a = b = c)	(a = ß = g 90^o)
Hexagonal	(a = b c)	(a = ß = 90^o, g = 120^o)
Triclinic	(a b c)	(a ß g 90^o)

The three cubic unit cells in the Bravais classification are particularly important for our purposes. As might be expected, the simple cubic unit cell is the simplest repeating unit in a simple cubic structure and the body-centered cubic unit cell is the simplest repeating unit in a body-centered cubic structure. The face-centered cubic unit cell is the simplest repeating unit in a cubic closest packed structure. In fact, the presence of face-centered cubic unit cells explains why this structure is known as cubic closest packed.

Look at the three structures below (Rotate them until you agree with the labels.)

The lattice points in a unit cell can be described in terms of a three-dimensional graph. For the sake of argument, let's define the a axis as the vertical axis of our coordinate system, as shown in the figure below. The b axis will describe movement across the front of the unit cell, and the c axis will represent movement toward the back of the unit cell. The bottom-left corner of the unit cell is now the origin (0,0,0) of our coordinate system. The coordinates 1,0,0 indicate a lattice point one cell-edge length away from the origin along the a axis. Similarly, 0,1,0 and 0,0,1 represent lattice points that are displaced by one cell-edge length from the origin along the b and c axes, respectively.

Thinking about the unit cell as a three-dimensional graph allows us to describe the structure of a crystal with a remarkably small amount of information. We can specify the structure of cesium chloride, for example, with only four pieces of information.

Because the cell edge must connect equivalent lattice points, the presence of a Cl^- ion at one corner of the unit cell (0,0,0) implies the presence of a Cl^- ion at every corner of the cell. The coordinates ½,½,½ describe a lattice point at the center of the cell. CsCl is therefore a simple-cubic unit cell of Cl^- ions with a Cs⁺in the center of the body of the cell, as shown in the figure below.

NaCl should crystallize in a cubic closest packed array of Cl^- ions with Na⁺ions in the octahedral holes between planes of Cl^- ions. We can translate this information into a unit-cell model for NaCl by remembering that the face-centered cubic unit cell is the simplest repeating unit in a cubic closest packed structure.

There are four unique positions in a face-centered cubic unit cell. These positions are defined by the coordinates: 0,0,0; 0,½,½; ½,0,½, and ½,½,0. The presence of a particle at one corner of the unit cell (0,0,0) requires the presence of an equivalent particle on each of the eight corners of the unit cell. Because the unit-cell edge connects equivalent points, the presence of a particle in the center of the bottom face (0,½,½) implies the presence of an equivalent particle in the center of the top face (1,½,½). Similarly, the presence of particles in the center of the ½,0,½ and ½,½,0 faces of the unit cell implies equivalent particles in the centers of the ½,1,½ and ½,½,1 faces.

The the unit cell labeled "a" in the figure below shows that there is an octahedral hole in the center of a face-centered cubic unit cell, at the coordinates ½,½,½. Any particle at this point touches the particles in the centers of the six faces of the unit cell.

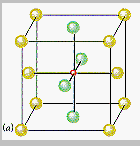
The other octahedral holes in a face-centered cubic unit cell are on the edges of the cell, such as the octahedral hole at the coordinates ½,0,0 shown in the figure below.

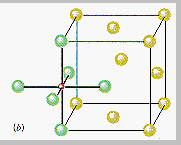
If Cl^- ions occupy the lattice points of a face-centered cubic unit cell and all of the octahedral holes are filled with Na⁺ions, we get the unit cell for NaCl shown in the figure below.

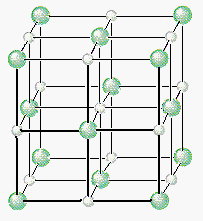
We can therefore describe the structure of NaCl in terms of the following information.

Placing a Cl^- ion at these four positions implies the presence of a Cl^- ion on each of the 14 lattice points that define a face-centered cubic unit. Placing a Na⁺ion in the center of the unit cell (½,½,½) and on the three unique edges of the unit cell (½,0,0; 0,½,0; and 0,0,½) requires an equivalent Na⁺ion in every octahedral hole in the unit cell.

ZnS will crystallize as cubic closest packed array of S^2- ions with Zn²⁺ions in tetrahedral holes. The S²ions in this crystal occupy the same positions as the Cl^- ions in NaCl. The only difference between these crystals is the location of the positive ions. The figure below shows that the tetrahedral holes in a face-centered cubic unit cell are in the corners of the unit cell, at coordinates such as ¼,¼,¼. An atom with these coordinates would touch the atom at this corner as well as the atoms in the centers of the three faces that form this corner. Although it is difficult to see without a three-dimensional model, the four atoms that surround this hole are arranged toward the corners of a tetrahedron.

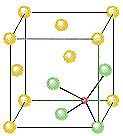
Because the corners of a cubic unit cell are identical, there must be a tetrahedral hole in each of the eight corners of the face-centered cubic unit cell. If S^2-ions occupy the lattice points of a face-centered cubic unit cell and Zn²⁺ions are packed into every other tetrahedral hole, we get the unit cell of ZnS shown in the figure below.

Note that only half of the tetrahedral holes are occupied in this crystal because there are two tetrahedral holes for every S^2-ion in a closest packed array of these ions.

The structure of a solid can be determined using a technique known as x-ray diffraction. X- rays that strike a crystal are reflected from different planes of atoms near the surface, as shown in the figure below.

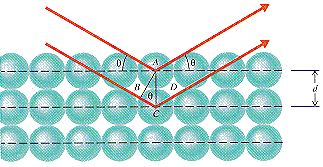
X-rays reflected from different planes of atoms are no longer in phase and they tend to cancel each other. They can only stay in phase if the extra distance (BC + CD) the x-ray moves when it strikes the second plane of atoms is equal to an integer (n) times the wavelength (

) of the radiation. Thus the sum of the distances labeled BC and CD in the figure above is equal to an integer times the wavelength of any radiation that has remained in phase.

The angle between the beam of x-rays and the planes of the crystal is defined as Q. Because the BAC angle is also equal to Q, the BC distance is equal to the AC distance times the sine of Q.

Because the AC distance is equal to the distance between planes of atoms, d, the relationship between the BC and AC distances can be written as follows.

Because the BC distance is equal to the CD distance, the following must be true.

Substituting the relationship between BC + CD and n gives a formula known as the Bragg equation, which allows us to calculate the distance between planes of atoms in a crystal from the pattern of diffraction of x-rays of known wavelength.

The Structure of Metals	Solid Solutions and Intermetallic Compounds	Holes in Closest Packed and Simple Cubic Structures	Radius Ratio Rules
Unit Cells: A Three-Dimensional Graph	Unit Cells: NaCl and ZnS	Unit Cells: Determining the Distance Between Particles

Materials Science