The Solubility Product Expression
Silver chloride is so insoluble in water (.0.002 g/L) that a saturated solution contains only about 1.3 x 10-5 moles of AgCl per liter of water.
| H2O | ||||
| AgCl(s) | Ag+(aq) | + | Cl-(aq) |
Strict adherence to the rules for writing equilibrium constant expressions for this reaction gives the following result.
![]()
(Water isn't included in the equilibrium constant expression because it is neither consumed nor produced in this reaction, even though it is a vital component of the system.)
The [Ag+] and [Cl-] terms represent the
concentrations of the Ag+ and Cl- ions in
moles per liter when this solution is at equilibrium. The third
term![]() [AgCl]
[AgCl]![]() is
more ambiguous. It doesn't represent the concentration of AgCl
dissolved in water because we assume that AgCl dissociates into
Ag+ ions and Cl- ions when it dissolves in
water. It can't represent the amount of solid AgCl in the system
because the equilibrium is not affected by the amount of excess
solid added to the system. The [AgCl] term has to be translated
quite literally as the number of moles of AgCl in a liter of
solid AgCl.
is
more ambiguous. It doesn't represent the concentration of AgCl
dissolved in water because we assume that AgCl dissociates into
Ag+ ions and Cl- ions when it dissolves in
water. It can't represent the amount of solid AgCl in the system
because the equilibrium is not affected by the amount of excess
solid added to the system. The [AgCl] term has to be translated
quite literally as the number of moles of AgCl in a liter of
solid AgCl.
The concentration of solid AgCl can be calculated from its density and the molar mass of AgCl.
![]()
This quantity is a constant, however. The number of moles per liter in solid AgCl is the same at the start of the reaction as it is when the reaction reaches equilibrium.
Since the [AgCl] term is a constant, which has no effect on the equilibrium, it is built into the equilibrium constant for the reaction.
[Ag+][Cl-] = Kc x [AgCl]
This equation suggests that the product of the equilibrium concentrations of the Ag+ and Cl- ions in this solution is equal to a constant. Since this constant is proportional to the solubility of the salt, it is called the solubility product equilibrium constant for the reaction, or Ksp.
Ksp = [Ag+][Cl-]
The Ksp expression for a salt is the product of the concentrations of the ions, with each concentration raised to a power equal to the coefficient of that ion in the balanced equation for the solubility equilibrium.
| Practice Problem 1: Write the Ksp expression for a saturated solution of CaF2 in water. |
The Relationship Between Ksp And the Solubility of a Salt
Ksp is called the solubility product because it is literally the product of the solubilities of the ions in moles per liter. The solubility product of a salt can therefore be calculated from its solubility, or vice versa.
Photographic films are based on the sensitivity of AgBr to light. When light hits a crystal of AgBr, a small fraction of the Ag+ ions are reduced to silver metal. The rest of the Ag+ ions in these crystals are reduced to silver metal when the film is developed. AgBr crystals that do not absorb light are then removed from the film to "fix" the image.
Example: Let's calculate the solubility of AgBr in water in grams per liter, to see whether AgBr can be removed by simply washing the film.
We start with the balanced equation for the equilibrium.
| H2O | ||||
| AgBr(s) | Ag+(aq) | + | Br-(aq) |
We then write the solubility product expression for this reaction.
Ksp = [Ag+][Br-] = 5.0 x 10-13
One equation can't be solved for two unknowns![]() the
Ag+ and Br- ion concentrations. We can
generate a second equation, however, by noting that one Ag+
ion is released for every Br- ion. Because there is no
other source of either ion in this solution, the concentrations
of these ions at equilibrium must be the same.
the
Ag+ and Br- ion concentrations. We can
generate a second equation, however, by noting that one Ag+
ion is released for every Br- ion. Because there is no
other source of either ion in this solution, the concentrations
of these ions at equilibrium must be the same.
[Ag+] = [Br-]
Substituting this equation into the Ksp expression gives the following result.
[Ag+]2 = 5.0 x 10-13
Taking the square root of both sides of this equation gives the equilibrium concentrations of the Ag+ and Br- ions.
[Ag+] = [Br-] = 7.1 x 10-7M
Once we know how many moles of AgBr dissolve in a liter of water, we can calculate the solubility in grams per liter.

The solubility of AgBr in water is only 0.00013 gram per liter. It therefore isn't practical to try to wash the unexposed AgBr off photographic film with water.
Solubility product calculations with 1:1 salts such as AgBr are relatively easy to perform. In order to extend such calculations to compounds with more complex formulas we need to understand the relationship between the solubility of a salt and the concentrations of its ions at equilibrium. We will use the symbol Cs to describe the amount of a salt that dissolves in water.
| Practice Problem 2: Several compounds were studied as possible sources of the fluoride ion for use in toothpaste. Write equations that describe the relationship between the solubility of CaF2 and the equilibrium concentrations of the Ca2+ and F- ions in a saturated solution as a first step toward evaluating its use as a fluoridating agent.
|
| Practice Problem 3: Use the Ksp for calcium fluoride to calculate its solubility in grams per liter. Comment on the potential of CaF2 to act as a fluoridating agent. (CaF2: Ksp = 4.0 x 10-11) |
The techniques used in the preceding practice problems are also valid for salts that contain more positive ions than negative ions.
| Practice Problem 4: Calculate the solubility in grams per liter of silver sulfide in order to decide whether it is accurately labeled when described as an insoluble salt. (Ag2S: Ksp = 6.3 x 10-50)
|
Common Misconceptions About Solubility Product Calculations
Let's focus on one step in Practice Problem 4. We started with the solubility product expression for Ag2S.
Ksp = [Ag+]2[S2-]
We then substituted the relationship between the concentrations of these ions and the solubility of the salt into this equation.
[2 Cs]2[Cs] = 6.3 x 10-50
When they see this for the first time, students often ask: "Why did you double the Ag+ ion concentration and then square it? Aren't you counting this term twice?"
This question results from confusion about the symbols used in the calculation. Remember that the symbol Cs in this equation stands for the solubility of Ag2S in moles per liter. Since we get two Ag+ ions for each Ag2S formula unit that dissolves in water, the Ag+ ion concentration at equilibrium is twice the solubility of the salt, or 2 Cs. We square the Ag+ ion concentration term because the equilibrium constant expression for this reaction is proportional to the product of the concentrations of the three products of the reaction.
Ksp = [Ag+][Ag+][S2-]
It is just more convenient to write this equation in the condensed form.
Ksp = [Ag+]2[S2-]
Another common mistake in solubility product calculations
occurs when students are asked to write an equation that
describes the relationship between the concentrations of the Ag+
and S2- ions in a saturated Ag2S solution.
It is all too easy to look at the formula for this compound![]() Ag2S
Ag2S![]() and
then write the following equation.
and
then write the following equation.
[S2-] = 2 [Ag+]
This seems reasonable to some, who argue that there are twice as many Ag+ ions as S2- ions in the compound. But the equation is wrong. Because two Ag+ ions are produced for each S2- ion, there are twice as many silver ions as sulfide ions in this solution. This solution is correctly described by the following equation.
[Ag+] = 2 [S2-]
How can you avoid making this mistake? After you write the equation that you think describes the relationship between the concentrations of the ions, try it to see if it works. Suppose just enough Ag2S dissolved in water to give two S2- ions. How many Ag+ ions would you get? Four. If you get the right answer when you substitute this concrete example into your equation, it must be written correctly.
Using Ksp As A Measure Of the Solubility of a Salt
The value of Ka for an acid is proportional to the strength of the acid.

If we find the following Ka values in a table, we can immediately conclude that formic acid is a stronger acid than acetic acid.
| Formic acid (HCO2H): | Ka = 1.8 x 10-4 | |
| Acetic acid (CH3CO2H): | Ka = 1.8 x 10-5 |
The same can be said about values of Kb.
![]()
The following base-ionization equilibrium constants imply that methylamine is a stronger base than ammonia.
| Methylamine (CH3NH2): | Kb = 4.8 x 10-4 | |
| Ammonia (NH3): | Kb = 1.8 x 10-5 |
Unfortunately, there is no simple way to predict the relative solubilities of salts from their Ksp's if the salts produce different numbers of positive and negative ions when they dissolve in water.
| Practice Problem 5: Determine
which salt
|
The Role of the Ion Product (Qsp) In Solubility Calculations
Consider a saturated solution of AgCl in water.
| H2O | ||||
| AgCl(s) | Ag+(aq) | + | Cl-(aq) |
Because AgCl is a 1:1 salt, the concentrations of the Ag+ and Cl- ions in this solution are equal.
| Saturated solution of AgCl in water: |
[Ag+] = [Cl-]
Imagine what happens when a few crystals of solid AgNO3 are added to this saturated solution of AgCl in water. According to the solubility rules, silver nitrate is a soluble salt. It therefore dissolves and dissociates into Ag+ and NO3- ions. As a result, there are two sources of the Ag+ ion in this solution.
| AgNO3(s) | Ag+(aq) | + | NO3-(aq) | |
| H2O | ||||
| AgCl(s) | Ag+(aq) | + | Cl-(aq) |
Adding AgNO3 to a saturated AgCl solution therefore increases the Ag+ ion concentrations. When this happens, the solution is no longer at equilibrium because the product of the concentrations of the Ag+ and Cl- ions is too large. In more formal terms, we can argue that the ion product (Qsp) for the solution is larger than the solubility product (Ksp) for AgCl.
Qsp = (Ag+)(Cl-) > Ksp
The ion product is literally the product of the concentrations of the ions at any moment in time. When it is equal to the solubility product for the salt, the system is at equilibrium.
The reaction eventually comes back to equilibrium after the excess ions precipitate from solution as solid AgCl. When equilibrium is reestablished, however, the concentrations of the Ag+ and Cl- ions won't be the same. Because there are two sources of the Ag+ ion in this solution, there will be more Ag+ ion at equilibrium than Cl- ions:
| Saturated solution of AgCl to which AgNO3 has been added: |
[Ag+] > [Cl-]
Now imagine what happens when a few crystals of NaCl are added to a saturated solution of AgCl in water. There are two sources of the chloride ion in this solution.
| H2O | ||||
| NaCl(s) | Na+(aq) | + | Cl-(aq) | |
| H2O | ||||
| AgCl(s) | Ag+(aq) | + | Cl-(aq) |
Once again, the ion product is larger than the solubility product.
Qsp = (Ag+)(Cl-) > Ksp
This time, when the reaction comes back to equilibrium, there will be more Cl- ion in the solution than Ag+ ion.
| Saturated solution of AgCl to which NaCl has been added: |
[Ag+] < [Cl-]
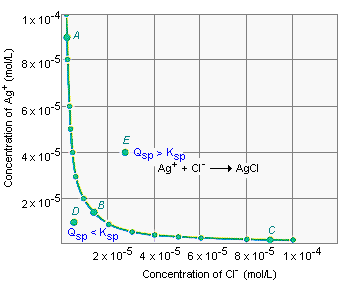
The figure below shows a small portion of the possible combinations of the Ag+ and Cl- ion concentrations in an aqueous solution. Any point along the curved line in this graph corresponds to a system at equilibrium, because the product of the Ag+ and Cl- ion concentrations for these solutions is equal to Ksp for AgCl.
Point A represents a solution at equilibrium that could
be produced by dissolving two sources of the Ag+ ion ![]() such
as AgNO3 and AgCl
such
as AgNO3 and AgCl ![]() in
water. Point B represents a saturated solution of AgCl in
pure water, in which the [Ag+] and [Cl-]
terms are equal. Point C describes a solution at
equilibrium that was prepared by dissolving two sources of the Cl-
ion in water, such as NaCl and AgCl.
in
water. Point B represents a saturated solution of AgCl in
pure water, in which the [Ag+] and [Cl-]
terms are equal. Point C describes a solution at
equilibrium that was prepared by dissolving two sources of the Cl-
ion in water, such as NaCl and AgCl.
Any point that is not along the solid line in the above figure represents a solution that is not at equilibrium. Any point below the solid line (such as Point D) represents a solution for which the ion product is smaller than the solubility product.
| Point D: | Qsp < Ksp |
If more AgCl were added to the solution at Point D, it would dissolve.
| If Qsp < Ksp: | AgCl(s) |
Points above the solid line (such as Point E) represent solutions for which the ion product is larger than the solubility product.
| Point E: | Qsp > Ksp |
The solution described by Point E will eventually come to equilibrium after enough solid AgCl has precipitated.
| If Qsp > Ksp: | Ag+(aq) + Cl-(aq)
|