Defects

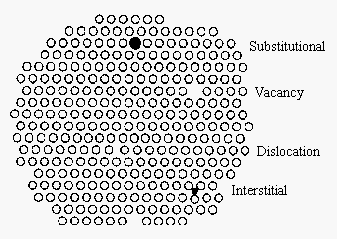
It is useful to think about solids in terms of a regular repeating pattern of planes of particles. But it is important to recognize that solids are seldom perfectly ordered. There are four basic mechanisms for introducing a point defect into the structure of a solid, as shown in the figure below. When a particle is missing at one or more lattice sites we get a vacancy. When a particle forces its way into a hole between lattice sites, we get an interstitial impurity. Substitutional impurities result from replacing the particle that should occupy a lattice site with a different particle, such as substituting a K⁺ ion for a Na⁺ ion in NaCl. (If an ion with a different charge is substituted, the electrical neutrality of the crystal must be maintained. If a Ca²⁺ ion is substituted for a Na⁺ ion, for example, a second Na⁺ ion must leave the crystal so that it doesn't pick up an electric charge.) Dislocations are one-dimensional defects caused by holes that are not large enough to be a vacancy.

When a significant fraction of the original particles are replaced by impurities, it is possible to get a solid solution. Alloys, such as bronze and brass, are examples of solid solutions. Bronze is a solution of tin dissolved in copper. Brass is a mixture of copper and zinc that can contain as little as 10%, or as much as 45%, zinc.

Distortions of the crystal lattice often occur when impurities are added to a solid. As a result, point defects often determine the properties of a material. They can change the ease with which a material conducts electricity, its mechanical strength, its ability to be shaped by hammering (malleability), or to be drawn into wires (ductility). Dissolving small amounts of carbon in iron, for example, give the alloy known as steel, which is significantly stronger than iron. But higher percentages of carbon make steel so brittle that it can shatter when dropped.

Point defects distort the lattice and provide a way for atoms to move about the solid. Atoms can move from a lattice site into a vacancy, for example, creating a new vacancy, as shown in the figure below.

Theoretical calculations of the ease with which one plane of atoms should slip over another suggest that metals should be much more resistant to stress than they are. In other words, metals are softer than one would expect. Metallurgists have explained this by assuming that metals contain defects that allow planes of atoms to slip past each other more readily than expected. This hypothesis has been confirmed by microscopic analysis, which shows dislocations that run through the crystal. There are two types of dislocations: edge or screw dislocations. An edge dislocation is an extra half plane of atoms that goes part way through a solid structure, as shown in the figure below.

Imagine, for example, a single playing card inserted halfway into a deck of cards. The line formed by the inserted card would be a dislocation line. The presence of a dislocation defect allows one plane of atoms to slip more easily over its neighboring plane of atoms, as shown in the figure below. Not all the atoms in the two planes move past each other simultaneously; they move one row at a time.

An often quoted analogy is that of moving a carpet. Dragging the carpet across the floor is difficult because of the friction developed from the contact of the surface of the carpet with the floor. Imagine what would happen, however, if a wrinkle is put into the carpet, as shown in part (a) of the figure below. The carpet can now be moved by pushing the wrinkle across the floor, because only the friction between a small section of carpet and the floor has to be overcome. A similar phenomenon occurs when one plane of atoms moves past another by means of a dislocation defect.

Because they allow planes of atoms in a solid to move one row at a time, dislocations can weaken a metal. Paradoxically, they can also strengthen a metal when the dislocations intersect to product knots similar to the intersecting wrinkles in the figure labeled "b" in the figure below. This phenomenon is encountered with metals that have been work hardened. Consider what happens, for example, when a piece of iron is heated, hammered, cooled, reheated, and reworked to form wrought iron. In the course of work hardening the metal, intersecting dislocations are generated that hinder the movement of planes of atoms.

Screw dislocations are more difficult to visualize than edge dislocations.The figure below shows how a screw dislocation is produced when one side of a crystal is displaced relative to the other side. For either edge or screw dislocations a distortion is produced around the dislocation with a corresponding stress produced within the material.

A significant fraction of the gross national product (GNP) of the United States, and all of the contribution to the GNP from high-technology industries, can be traced to efforts to harness differences in the way metals, semiconductors, and insulators conduct electricity. This difference can be expressed in terms of electrical conductivity, which measures the ease with which materials conduct an electric current. It can also be expressed in terms of electrical resistivity, the inverse of conductivity, which measures the resistance of a material to carrying an electric charge.

Silver and copper metal are among the best conductors of electricity, with a conductivity of only 10⁶ohm-cm. (This is why copper is the metal most often used in electric wires.) The conductivity of semiconductors such as silicon and germanium is 10⁸ to 10¹⁰ times smaller. (When pure, these semimetals have a conductivity of 10^-2 to 10^-4 ohm-cm.) Insulators include glass (10^-10ohm-cm), diamond (10^-14 ohm-cm), and quartz (10^-18 ohm-cm), which all have an extremely small tendency to carry an electric current.

The 10²⁴-fold range of conductivity is not the only difference among metals, semiconductors, and insulators. Metals become better conductors when they are cooled to lower temperatures. Some metals are such good conductors at very low temperatures that they no longer have a measurable resistance and therefore become superconductors. Semiconductors show the opposite behavior they become much better conductors as the temperature increases. The difference between the temperature dependence of metals and semiconductors is so significant it is often the best criterion for distinguishing between these materials. The large range of conductivities of solids is shown in the figure below.

Semiconductors are very sensitive to impurities. The conductivity of silicon or germanium can be increased by a factor of up to 10⁶ by adding as little as 0.01% of an impurity. Metals, on the other hand, are fairly insensitive to impurities. It takes a lot of impurity to change the conductivity of a metal by as much as a factor of 10; and unlike semiconductors, metals become poorer conductors when impure.

To explain the behavior of metals, semiconductors, and insulators, we need to understand the bonding in solids in more detail. Because it is the lightest element in the period table that is a solid at room temperature, let's start by building a model of what happens when lithium atoms interact. As a first step, we can consider what happens when a pair of lithium atoms with a 1s² 2s¹configuration interact to form a hypothetical gas phase Li₂ molecule. The Li₂ molecule is formed by placing two electrons in the bonding domain between the two Li nuclei.

Now let's imagine what happens when enough lithium atoms come together to form a piece of lithium metal. The valence electrons are no longer confined to the region between pairs of lithium nuclei, as was the case for an isolated Li₂ molecule in the gas phase. In the metal, each lithium atom is perturbed by its neighbors and the energy states of each atom are slightly altered. The 1s orbitals on the various metal atoms interact to form a band of orbitals whose energy falls within a range from slightly below the energy of the isolated 1s orbital to slightly above this energy, as shown in the figure below. The same thing happens to the 2s orbitals.

Each of the orbitals in these bands can hold two electrons of opposite spin. Because there were two electrons in each of the 1s orbitals that formed the lower-energy band, the "1s" band is filled. But there was only one electron in each of the 2s orbitals that formed the higher-energy band, which means that the "2s" band is only half-filled. It takes little, if any energy, to excite one of the electrons in the 2s band from one orbital to another in the band. (The energy gap between orbitals in the 2s band in lithium is only about 10^-45 kJ.) By moving from orbital to orbital within the 2s band, electrons can move from one end of the crystal to the other. This band of orbitals is therefore called a conduction band because it enables lithium metal to conduct electricity.

Let's now turn to magnesium, which has a [Ne] 3 s²configuration. The 3s orbitals on the neighboring magnesium atoms would overlap to form a band of 3s orbitals. Because there are two electrons in each 3s orbital, this band is totally filled. The empty 3p orbitals on magnesium, however, also interact to form a band of orbitals. This empty 3p overlaps the 3s band in magnesium, so that the combined band is only partially filled, allowing magnesium to conduct electricity.

The differences in the way metals, semiconductors, and insulators conduct electricity can be explained with the diagram in the figure below. Metals have filled bands of core electrons, such as the 1s band in lithium or the 1s and 2s bands in magnesium. But they also have partially filled bands of orbitals that allow electrons to move from one end of the crystal to the other. They therefore conduct an electric current. All of the bands in an insulator are either filled or empty. Furthermore, the gap between the highest energy filled band and the lowest energy empty band in an insulator is so large that it is difficult to excite electrons from one of these bands to the other. As a result, it is difficult to move electrons through an insulator.

Semiconductors also have a band structure that consists of filled and empty bands. The gap between the highest energy filled band and the lowest energy empty band is small enough, however, that electrons can be excited into the empty band by the thermal energy the electrons carry at room temperature. Semiconductors therefore fall between the extremes of metals and insulators in their ability to conduct an electric current.

To understand why metals become better conductors at low temperature it is important to remember that temperature is a macroscopic reflection of the kinetic energy of the individual particles. Much of the resistance of a metal to an electric current at room temperature is the result of scattering of the electrons by the thermal motion of the metal atoms as they vibrate back and forth around their lattice points. As the metal is cooled, and this thermal motion slows down, there is less scattering, and the metal becomes a better conductor.

Semiconductors become better conductors at high temperatures because the number of electrons with enough thermal energy to be excited from the filled band to the empty band increases.

To understand why semiconductors are sensitive to impurities, let's look at what happens when we add a small amount of a Group VA element, such as arsenic, to one of the Group IVA semiconductors. Arsenic atoms have one more valence electron than germanium and silicon atoms. Arsenic atoms can therefore lose an electron to form As⁺ ions that can occupy some of the lattice points in the crystal where silicon or germanium atoms are normally found.

If the amount of arsenic is kept very small, the distance between these atoms is so large that they don't interact. As a result, the extra electrons from the arsenic atoms occupy orbitals in a very narrow band of energies that lie between the filled and empty bands of the semiconductor, as shown in the figure below. This decreases the amount of energy required to excite an electron into the lowest energy empty band in the semiconductor and therefore increases the number of electrons that have enough energy to cross this gap. As a result, this "doped" semiconductor becomes a very much better conductor of electricity than the pure semiconductor. Because the electric charge is carried by a flow of negative particles, these semiconductors are called n-type.

It is also possible to dope a Group IVA semiconductor with one of the elements in Group IIIA, such as indium. These atoms have one less valence electron than silicon or germanium atoms, and they can capture electrons from the highest energy filled band to form holes in this band. The presence of holes in a filled band has the same effect as the presence of electrons in an empty band it allows the solid to carry an electric current. The electric charge is now carried by a flow of positive particles, or holes, so these semiconductors are called p-type.

Bringing n-type and p-type semiconductors together produces a device that has a natural one-directional flow of electrons, which can be turned off by applying a small voltage in the opposite direction. This junction between n-type and p-type semiconductors was the basis of the revolution in industrial technology that followed the discovery of the transistor by William Shockley, John Bardeen, and Walter Brattain at Bell Laboratories in 1948.

You may have noticed that metal ice-cube trays feel significantly colder then plastic ice-cube trays when you remove them from the freezer. Your senses are obviously misleading you because the trays are at the same temperature the temperature of the freezer. The metal trays feel colder because metals are much better conductors of heat than plastic.

The ease with which metals conduct heat is related to their ability to conduct an electric current. Most of the energy absorbed by a metal when it is heated is used to increase the rate at which the atoms vibrate around their lattice sites. But some of this energy is absorbed by electrons in the metal, which move from orbital to orbital through the conduction band. The net result is a transport of kinetic energy from one portion of the metal surface to another. Metals feel cold to the touch because the electrons in the conduction band carry heat away from our bodies and distribute this energy through the metal object.

Plastics, on the other hand, are thermal insulators. They are poor conductors of heat because orbitals in which electrons are held tend to be localized on an individual atom or between pairs of atoms. The only way for electrons to carry energy through a plastic is to use this energy to excite an electron from a filled orbital to an empty orbital. But the difference between the energies of the filled and empty orbitals is so large that this rarely happens.

The difference between thermal conductors and thermal insulators can be quantified by defining the thermal conductivity of a substance as the quantity of heat transmitted per second through a plate of the material one centimeter thick and one square centimeter in area when the temperature differential between the two sides of the plate is one degree Celsius or one Kelvin. The copper used to for pots and pans has a thermal conductivity that is more than 5000 times the value for the styrofoam used for coffee cups, as shown by the data in the table below. This table is consistent with experience, which suggests that the air that gets trapped in the fibers of a down-filled jacket is a better insulator than cotton, which is a much better insulator than nylon.

Material	Thermal Conductivity (J/s·cm·K)^a	Material	Thermal Conductivity (J/s·cm·K)^a
Air	0.00026	Pb	0.353
Glass wool	0.00042		Cs 0.359
Cotton	0.00057		MgO 0.360 (100°F)
Styrofoam	0.00079	Rb	0.582
Carbon tetrachoride	0.0010	Fe	0.804
White pine	0.0011	Li	0.848
Oak	0.0015	K	1.025
He	0.001520	C (graphite)^b	1.1-2.2
Cardboard	0.0021	Zn	1.16
Nylon	0.0025	Brass	1.2
Water	0.0061	Na	1.42
Brick	0.0063	Mg	1.56
Glass	0.0072-0.0088	Be	2.01
Concrete	0.0086-0.013	BeO	2.20 (100°F)
Hg	0.083	Al	2.37
SiC	0.090 (100°F)	Au	3.18
NaCl	0.092 (0°C)	Cu	4.01
ZnS (zinc blend)	0.264 (0°C)	Ag	4.29
Al₂O₃	0.303 (100°C)	C (diamond)^c	9.9-23.2
^aAll values are at room temperature unless otherwise noted. ^bValue is dependent on the impurities in graphite and on the orientation of graphite, being larger in the direction parallel to the layers of carbon atoms. ^cValue is highly dependent on impurities and defects.

It is tempting to think about solids as if the particles were locked into position, the way bricks are used to build a wall. This would be a mistake, however, because the particles in a solid are in more or less constant motion rocking back and forth and rotating about their fixed positions in the crystal. This motion depends on two factors, the temperature of the system and the strength of the interactions that hold the particles together. The higher the temperature, the faster the particles are moving. The stronger the force of attraction between particles, the smaller the distances the particles move apart. Because the van der Waals forces that hold molecules together are much weaker than the bonds between atoms in a metal or between positive and negative ions in an ionic compound, molecular crystal expand more when heated than metals or ionic compounds.

The difference between the coefficients of thermal expansion of iron and copper was the source of a major problem for the Statue of Liberty, which consists of copper plates supported by an iron skeleton. The insulating material used to keep these two metals from coming into contact was inevitably rubbed away because of differences in the rate at which these two metals expand when heated and contract when cooled. (For each degree change in the temperature of the Statue, the volume of the copper metal changes by 40% more than the iron metal.) When this happened, the two metals came into contact, forming an electric cell that greatly increased the rate at which the iron skeleton corroded.

The same phenomenon, however, is used to form the thermostats that turn electrical appliances on and off. When two metals with very different coefficients of thermal expansion are joined to form a bimetallic strip, the metal that expands the most when heated forces the adjoined metal strip to bend toward the metal with the smallest thermal expansion. This bimetallic strip can be used to make a device that will turn a heater on or off as contact is made or broken with an electrical contact, as shown in the figure below.

Thermal expansion and thermal conductivity can work together to weaken a material. If heat isn't transported quickly through an object that is heated, one part expands more rapidly than another. If any cracks or flaws are present, the hotter part of the substance will pull on the colder part and widen the crack, causing breakage.

Defects	Metals, Semiconductors, and Insulators
Thermal Conductivity	Thermal Expansion

Materials Science