| Octahedral Crystal Fields | Tetrahedral Crystal Fields | Square Planar Complexes |
| The Spectrochemical Series | High-Spin Versus Low-Spin Octahedral Complexes | |
At almost exactly the same time that chemists were developing the valence-bond model for coordination complexes, physicists such as Hans Bethe, John Van Vleck, and Leslie Orgel were developing an alternative known as crystal field theory. This theory tried to describe the effect of the electrical field of neighboring ions on the energies of the valence orbitals of an ion in a crystal. Crystal field theory was developed by considering two compounds: manganese(II) oxide, MnO, and copper(I) chloride, CuCl.
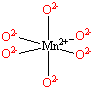
Each Mn2+ ion in manganese(II) oxide is surrounded by six O2- ions arranged toward the corners of an octahedron, as shown in the figure below. MnO is therefore a model for an octahedral complex in which a transition-metal ion is coordinated to six ligands.
What happens to the energies of the 4s and 4p orbitals on an Mn2+ ion when this ion is buried in an MnO crystal? Repulsion between electrons that might be added to these orbitals and the electrons on the six O2- ions that surround the metal ion in MnO increase the energies of these orbitals. The three 4p orbitals are still degenerate, however. These orbitals still have the same energy because each 4p orbital points toward two O2- ions at the corners of the octahedron.
Repulsion between electrons on the O2- ions and electrons in the 3d orbitals on the metal ion in MnO also increases the energy of these orbitals. But the five 3d orbitals on the Mn2+ ion are no longer degenerate. Let's assume that the six O2- ions that surround each Mn2+ ion define an XYZ coordinate system. Two of the 3d orbitals (3dx2-y2 and 3dz2) on the Mn2+ ion point directly toward the six O2- ions, as shown in the figure below. The other three orbitals (3dxy, 3dxz, and 3dyz) lie between the O2- ions.
The energy of the five 3d orbitals increases when the six O2- ions are brought close to the Mn2+ ion. However, the energy of two of these orbitals (3dx2-y2 and 3dz2) increases much more than the energy of the other three (3dxy, 3dxz, and 3dyz), as shown in the figure below. The crystal field of the six O2- ions in MnO therefore splits the degeneracy of the five 3d orbitals. Three of these orbitals are now lower in energy than the other two.
By convention, the dxy, dxz, and dyz orbitals in an octahedral complex are called the t2g orbitals. The dx2-y2 and dz2 orbitals, on the other hand, are called the eg orbitals.
The easiest way to remember this convention is to note that there are three orbitals in the t2g set.
| t2g: | dxy, dxz, and dyz | eg: | dx2-y2 and dz2 |
The difference between the energies of the t2g
and eg orbitals in an octahedral complex
is represented by the symbol ![]() o. This splitting
of the energy of the d orbitals is not trivial;
o. This splitting
of the energy of the d orbitals is not trivial; ![]() o
for the Ti(H2O)63+ ion, for
example, is 242 kJ/mol.
o
for the Ti(H2O)63+ ion, for
example, is 242 kJ/mol.
The magnitude of the splitting of the t2g and eg orbitals changes from one octahedral complex to another. It depends on the identity of the metal ion, the charge on this ion, and the nature of the ligands coordinated to the metal ion.
Each Cu+ ion in copper(I) chloride is surrounded by four Cl- ions arranged toward the corners of a tetrahedron, as shown in the figure below. CuCl is therefore a model for a tetrahedral complex in which a transition-metal ion is coordinated to four ligands.

Once again, the negative ions in the crystal split the energy of the d atomic orbitals on the transition-metal ion. The tetrahedral crystal field splits these orbitals into the same t2g and eg sets of orbitals as does the octahedral crystal field.
| t2g: | dxy, dxz, and dyz | eg: | dx2-y2 and dz2 |
But the two orbitals in the eg set are now lower in energy than the three orbitals in the t2g set, as shown in the figure below.

To understand the splitting of d orbitals in a tetrahedral crystal field, imagine four ligands lying at alternating corners of a cube to form a tetrahedral geometry, as shown in the figure below. The dx2-y2 and dz2 orbitals on the metal ion at the center of the cube lie between the ligands, and the dxy, dxz, and dyz orbitals point toward the ligands. As a result, the splitting observed in a tetrahedral crystal field is the opposite of the splitting in an octahedral complex.

Because a tetrahedral complex has fewer ligands, the magnitude
of the splitting is smaller. The difference between the energies
of the t2g and eg
orbitals in a tetrahedral complex (![]() t) is slightly less
than half as large as the splitting in analogous octahedral
complexes (
t) is slightly less
than half as large as the splitting in analogous octahedral
complexes (![]() o).
o).
![]() t = 4/9
t = 4/9 ![]() o
o
The crystal field theory can be extended to square-planar complexes, such as Pt(NH3)2Cl2. The splitting of the d orbitals in these compounds is shown in the figure below.

The splitting of d orbitals in the crystal field model not only depends on the geometry of the complex, it also depends on the nature of the metal ion, the charge on this ion, and the ligands that surround the metal. When the geometry and the ligands are held constant, this splitting decreases in the following order.
| Pt4+ | > | Ir3+ | > | Rh3+ | > | Co3+ | > | Cr3+ | > | Fe3+ | > | Fe2+ | > | Co2+ | > | Ni2+ | > | Mn2+ | |
| strong-field ligands | weak-field ligands | ||||||||||||||||||
Metal ions at one end of this continuum are called strong-field ions, because the splitting due to the crystal field is unusually strong. Ions at the other end are known as weak-field ions.
When the geometry and the metal are held constant, the splitting of the d orbitals decreases in the following order.
| CO | CN- | > | NO2- | > | NH3 | > | -NCS- | > | H2O | > | OH- | F- | -SCN- | Cl- | > | Br- | |||||
| strong-field ligands | weak-field ligands | ||||||||||||||||||||
Ligands that give rise to large differences between the energies of the t2g and eg orbitals are called strong-field ligands. Those at the opposite extreme are known as weak-field ligands.
Because they result from studies of the absorption spectra of
transition-metal complexes, these generalizations are known as
the spectrochemical series. The range of values of ![]() for
a given geometry is remarkably large. The value of
for
a given geometry is remarkably large. The value of ![]() o
is 100 kJ/mol in the Ni(H2O)62+
ion, for example, and 520 kJ/mol in the Rh(CN)63-
ion.
o
is 100 kJ/mol in the Ni(H2O)62+
ion, for example, and 520 kJ/mol in the Rh(CN)63-
ion.
High-Spin Versus Low-Spin Octahedral Complexes
Once we know the relative energies of the d orbitals in a transition-metal complex, we have to worry about how these orbitals are filled. Degenerate orbitals are filled according to Hund's rules.
- One electron is added to each of the degenerate orbitals in a subshell before a second electron is added to any orbital in the subshell.
- Electrons are added to a subshell with the same value of the spin quantum number until each orbital in the subshell has at least one electron.
Octahedral transition-metal ions with d1, d2, or d3 configurations can therefore be described by the following diagrams.

When we try to add a fourth electron, we are faced with a problem. This electron could be used to pair one of the electrons in the lower energy (t2g) set of orbitals or it could be placed in one of the higher energy (eg) orbitals. One of these configurations is called high-spin because it contains four unpaired electrons with the same spin. The other is called low-spin because it contains only two unpaired electrons. The same problem occurs with octahedral d5, d6, and d7 complexes.

For octahedral d8, d9, and d10 complexes, there is only one way to write satisfactory configurations.

As a result, we have to worry about high-spin versus low-spin octahedral complexes only when there are four, five, six, or seven electrons in the d orbitals.
The choice between high-spin and low-spin configurations for octahedral d4, d5, d6, or d7 complexes is easy. All we have to do is compare the energy it takes to pair electrons with the energy it takes to excite an electron to the higher energy (eg) orbitals. If it takes less energy to pair the electrons, the complex is low-spin. If it takes less energy to excite the electron, the complex is high-spin.
The amount of energy required to pair electrons in the t2g
orbitals of an octahedral complex is more or less constant. The
amount of energy needed to excite an electron into the higher
energy (eg) orbitals, however, depends
on the value of ![]() o for the complex. As a result,
we expect to find low-spin complexes among metal ions and ligands
that lie toward the high-field end of the spectrochemical series.
High-spin complexes are expected among metal ions and ligands
that lie toward the low-field end of these series.
o for the complex. As a result,
we expect to find low-spin complexes among metal ions and ligands
that lie toward the high-field end of the spectrochemical series.
High-spin complexes are expected among metal ions and ligands
that lie toward the low-field end of these series.

Compounds in which all of the electrons
are paired are diamagnetic![]() they
are repelled by both poles of a magnet. Compounds that contain
one or more unpaired electrons are paramagnetic
they
are repelled by both poles of a magnet. Compounds that contain
one or more unpaired electrons are paramagnetic![]() they
are attracted to the poles of a magnet. The force of attraction
between paramagnetic complexes and a magnetic field is
proportional to the number of unpaired electrons in the complex.
We can therefore determine whether a complex is high-spin or
low-spin by measuring the strength of the interaction between the
complex and a magnetic field.
they
are attracted to the poles of a magnet. The force of attraction
between paramagnetic complexes and a magnetic field is
proportional to the number of unpaired electrons in the complex.
We can therefore determine whether a complex is high-spin or
low-spin by measuring the strength of the interaction between the
complex and a magnetic field.
| Practice Problem 5: Explain why the Co(NH3)63+ ion is a diamagnetic, low-spin complex, whereas the CoF63- ion is a paramagnetic, high-spin complex. |